1

I am preparing for trading interviews and met this problem that essentially boiled down to computing/estimating (they key is speed) the expected value of the maximum face of two independent dice rolls. I understand that you may compute it through the formula $E[X] = \sum_{n} nP\{X \geq n\}$. However, I think it is not that fast. Is there any trick that people use to quickly get a sense of this problem? Thank you in advance!

Ziyang Guo
  • 153
  • I don't know about quick, but here's a discussion: https://math.stackexchange.com/questions/2439100/expected-value-of-the-max-of-2-dice – Matti P. Apr 09 '20 at 07:37

2 Answers2

1

Well it is always trade off between accuracy and speed right.

Our sense tell us that higher $X$ has higher probability and it is roughly proportional to $X$ (since if my highest die give me $X$, the other die can be anything from $1$ to $X$)

$1+2+...+6=21$ and $1+2+...+4=10 < \frac{21}{2}$ and $1+2+...+5=15 > \frac{21}{2}$. Thus the expected value may be between $4$ and $5$ since the median is between $4$ and $5$. If I do not have time, I will just say $4.5$.

The real expected value is $\frac{\sum_{i=1}^{6}{(2i^{2}-i)}}{36}=4.47...$ not bad!

acat3
  • 11,897
  • This is really helpful! I think your estimation is accurate enough for interview purposes especially under time pressure – Ziyang Guo Apr 10 '20 at 14:32
0

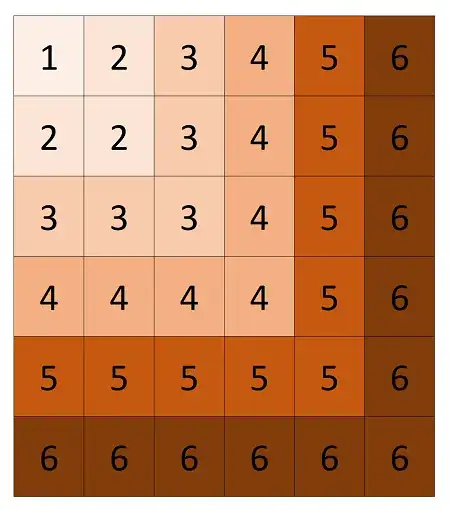
The simplest thing here is to view the problem graphically. For a pair of standard six-sided dice you can visualise the maximum value in a grid as shown below. You can see that the number of values of each number increases by the odd numbers --- $1, 3, 5, 7, ..., 11$. For dice with more sides, this pattern continues, with a longer series of odd numbers.

enter image description here

Using this pattern, we can see that for a pair of $w$-sided dice the expected value of the maximum roll is:

$$\begin{aligned} \mathbb{E}(M) = \sum_{m=1}^w m \cdot \frac{2m-1}{w^2} &= 1 \times \frac{1}{w^2} + 2 \times \frac{3}{w^2} + 3 \times \frac{5}{w^2} + \cdots + w \times \frac{2w-1}{w^2}. \\[6pt] \end{aligned}$$

Computing this expectation requires us to compute the sum of products of natural numbers and the corresponding odd numbers. The exact formula is:

$$\begin{aligned} \mathbb{E}(M) = \frac{1}{w^2} \sum_{m=1}^w m (2m-1) &= \frac{1}{w^2} \Bigg[ \frac{w(w+1)(2w+1)}{3} - \frac{w(w+1)}{2} \Bigg] \\[6pt] &= \frac{1}{w^2} \cdot \frac{2w(w+1)(2w+1)-3w(w+1)}{6} \\[6pt] &= \frac{1}{w^2} \cdot \frac{w(w+1)(4w-1)}{6} \\[6pt] &= \frac{(w+1)(4w-1)}{6w}. \\[6pt] &= \frac{4w + 3w-1}{6w}. \\[6pt] \end{aligned}$$

For a six-sided dice we have $w=6$ so that:

$$\mathbb{E}(M) = \frac{4 \cdot 6^2 + 3 \cdot 6 - 1}{6 \cdot 6} = \frac{144 + 18 - 1}{36} = \frac{161}{36} = 4.47 \bar{2}.$$

If you are looking for a quick-and-dirty approximation, you could approximate this sum by an integral:

$$\begin{aligned} \mathbb{E}(M) &\approx \int \limits_0^w m \cdot \frac{2m-1}{w^2} dm \\[6pt] &= \frac{1}{w^2} \int \limits_0^w (2m^2-m) dm \\[6pt] &= \frac{1}{w^2} \bigg[ \frac{2}{3} m^3 - \frac{1}{2} m^2 \bigg]_{m=0}^{m=w} \\[6pt] &= \frac{2}{3} w - \frac{1}{2} \\[6pt] &= \frac{4w^2-3w}{6w}. \\[6pt] \end{aligned}$$

This is quite close to the exact formula; only the last term in the formula is missing.

Ben
  • 4,079