Prove: $\frac{\sin{nx}}{\sin{x}}\geqslant{n-\frac{n(n^2-1)x^2}{6}},n\in{\mathbb{N}\setminus\{0\}, x\in{\mathbb{R}, x\neq k\pi}} $

Question

Prove : $\frac{\sin{nx}}{\sin{x}}\geqslant{n-\frac{n(n^2-1)x^2}{6}},n\in{\mathbb{N\setminus\{0\}}}, x\in{\mathbb{R}} $

I proved this relationship by incident. I tried to directly prove this afterwards, but failed. I would love to see another proof to this Problem.

-A proof-: we know that $\displaystyle\sum_{i=1}^{n}\cos{a_i}= \sum_{k=1}^{n}\cos{(a+(k-1)x)}=\frac{\cos{\frac{a+a_n}{2}}\sin{\frac{nx}{2}}}{\sin{\frac{x}{2}}}=T(x)\quad(1)$
(Here's the source for $(1)$). Also, $\displaystyle\sum_{i=1}^{n}a^2_i=\sum_{k=1}^{n}(a+(k-1)x)^2\\=\displaystyle\sum_{k=1}^{n}(a^2+2ax(k-1)+x^2(k-1)^2)\\=\displaystyle\sum_{k=1}^{n}a^2+2ax\sum_{k=1}^{n}(k-1)+x^2\sum_{k=1}^{n}(k-1)^2\\=na^2+2ax\frac{n(n-1)}{2}+x^2\frac{n(n-1)(2n-1)}{6}\quad(2)$

We consider the function $f(x)=\frac{x^2}{2}+\cos{x}\implies f''(x)=1-\cos{x}\geq{0}$ therefore $f(x)$ is a concave function. From Jensens inequality for concave functions:$ \displaystyle\sum_{i=1}^{n}f(a_i)\geq{nf\left(\frac{\sum_{i=1}^{n}a_i}{n}\right)}\iff\displaystyle\sum_{i=1}^{n}\left(\frac{a^2_i}{2}+\cos{a_i}\right)\geq n\Big(\frac{1}{2}\left(\frac{\frac{n}{2}(a+a_n)}{n}\right)^2+\cos{\frac{\frac{n}{2}(a+a_n)}{n}}\Big)\iff\frac{1}{2}\sum_{i=1}^{n}a^2_i+\sum_{i=1}^{n}\cos{a_i}\geq \frac{n}{2}\left(\frac{a+a_n}{2}\right)^2+n\cos{\frac{a+a_n}{2}}\overset{(1),(2)}{\iff}\frac{1}{2}\left(na^2+2ax\frac{n(n-1)}{2}+x^2\frac{n(n-1)(2n-1)}{6}\right)+T(x)\geqslant \frac{n\left(2a+(n-1)x\right)^2}{8}+n\cos{\frac{a+a_n}{2}}\overset{\ldots}{\iff} \frac{x^2n(n^2-1)}{3}\geqslant n\cos{\frac{a+a_n}{2}}-T(x)\overset{(1)}{\iff} \frac{x^2n(n^2-1)}{3}\geq \cos{\frac{a+a_n}{2}}\left(n-\frac{\sin{\frac{nx}{2}}}{\sin{\frac{x}{2}}}\right)\iff \frac{x^2n(n^2-1)}{3}\geqslant \cos{\left(a+\frac{(n-1)x}{2}\right)}\left(n-\frac{\sin{\frac{nx}{2}}}{\sin{\frac{x}{2}}}\right)\quad(3) $

$Lemma.$ For every dinstict $x,x\in\mathbb{R}_{\neq kπ}$ there exists at least one value of $a$ such that $\cos{(a+\frac{(n-1)x}{2}})=1\quad(5)$

Proof of the lemma: $(5)\iff (n-1)x=2-2a+4kπ\iff a=2kπ+1-\frac{(n-1)x}{2}$.

Hence, for every $x,x\in\mathbb{R}_{\neq k\pi}$ we have $\frac{x^2n(n^2-1)}{3}\geqslant \cos{\left(a+\frac{(n-1)x}{2}\right)}\left(n-\frac{\sin{\frac{nx}{2}}}{\sin{\frac{x}{2}}}\right)\overset{(4,x\to 2x)}{\iff}\frac{\sin{nx}}{\sin{x}}\geqslant{n-\frac{n(n^2-1)x^2}{6}} \square$

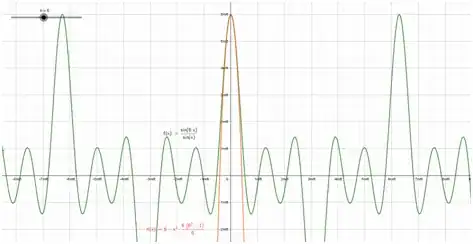
• To me it looks like $n-\frac{x^2n(n^2-1)}{6}$ is a good approximation function of $\frac{\sin{nx}}{\sin{x}}$ for small values of $x$ (or for small values of $x+ z\pi$, $z\in\mathbb{Z}$, it depends on $n$, because the second one is periodic with period multiple of $\pi$).

Answer 1

We will prove a more general result.

Let $$ f(x)=\frac{\sin nx}{\sin x}=\sum_{k=0}^\infty a_kx^{2k}\tag1 $$ and $$ f_m(x)=\sum_{k=0}^m a_kx^{2k}.\tag2 $$ Then the following inequalities hold: $$\begin{cases} f(x)\le f_m(x),& m\text{ even}\\ f(x)\ge f_m(x),& m\text{ odd}\\ \end{cases}.\tag3 $$

Your inequality will then follow as a special case: $m=1$.

The first key point of the proof is the observation: $$ \frac{\sin nx}{\sin x}=\sum_{\ell=0}^{n-1}e^{i(n-1-2\ell)x} =\begin{cases} 1+2\sum_{\ell=1}^{\frac{n-1}2}\cos2\ell x,&n\text{ odd}\\ 2\sum_{\ell=1}^{\frac{n}2}\cos(2\ell-1)x,&n\text{ even},\tag4 \end{cases} $$ which follows from simple telescopic identity: $$ (e^{ix}-e^{-ix})\sum_{\ell=0}^{n-1}e^{i(n-1-2\ell)x}=e^{inx}-e^{-inx}. $$

The second key point is the well-known inequalities (which can be proved e.g. by $2m$-fold integration of the inequality $1-\cos x\ge0$): $$ \begin{cases} \cos x\le \sum_{k=0}^m c_kx^{2k},& m\text{ even}\\ \cos x\ge \sum_{k=0}^m c_kx^{2k},& m\text{ odd}, \end{cases}\tag5 $$ where $c_k=\frac{(-1)^k}{(2k)!}$.

In view of (4) and (5) the relation (3) is proved.

As a byproduct of the proof one obtains a simple expression for the coefficients of the series expansion (1): $$ a_k=[x^{2k}]\frac{\sin nx}{\sin x}=[x^{2k}]\sum_{\ell=0}^{n-1}e^{i(n-1-2\ell)x}=\frac{(-1)^k}{(2k)!}\sum_{\ell=0}^{n-1}(n-1-2\ell)^{2k}.\tag6 $$

Particularly, $a_0=n$, $a_1=-\frac{n(n^2-1)}6$, and so on.

Answer 2

Remark: My previous solution is ugly. I give another solution.

Clearly, we only need to prove the case when $x > 0$.

For $n=1$, clearly the inequality is true.

For $n=2$, the inequality is equivalent to $2\cos x - 2 + x^2\ge 0$ which is true.

For $n\ge 3$ and $x\in [\frac{\pi}{2}, \infty)$: It is easy to prove that $-n \le \frac{\sin nx}{\sin x} \le n$ (by math induction) and $-n \ge n - \frac{n(n^2-1)x^2}{6}$. The inequality is true.

For $n \ge 3$ and $x\in (0, \frac{\pi}{2})$: Let $f(n) \triangleq \frac{\sin nx}{\sin x} - n + \frac{n(n^2-1)x^2}{6}$. We have \begin{align} f(n+2) - 2f(n+1) + f(n) &= \frac{-4(\sin\frac{x}{2})^2\sin (n+1) x}{\sin x} + (n+1)x^2\\ &\ge -4(n+1)(\sin\frac{x}{2})^2 + (n+1)x^2\\ & \ge 0 \end{align} where we have used $\sin (n+1) x \le (n+1)\sin x$. Thus, we have $f(n+2) - f(n+1) \ge f(n+1) - f(n)$ for all $n\ge 3$.
Thus, we have \begin{align} f(n+1) - f(n) &\ge f(4) - f(3) \\ &= 8(\cos x)^3- 4(\cos x)^2+6x^2-4\cos x\\ &= 2(4\cos x + 3)(1-\cos x)^2 + 6x^2 - 6(\sin x)^2\\ & \ge 0. \end{align}
Thus, we have $f(n) \ge f(3) = -4(\sin x)^2+4x^2\ge 0$ for all $n\ge 3$.

We are done.

Answer 3

Let $f(n,x)=n-\frac{(n-1)n(n+1)}{6}x^2$ the RHS of the required inequality. Wlog we can ssume $n \ge 3$ as for $n=1,2$ the inequality is trivial ($n=2$ reduces to $2\sin^2(\frac{x}{2}) \le \frac{x^2}{2}$ which follows from $|\sin x| \le |x|$).

Using the well known inequality $|\frac{\sin nx}{\sin x}| \le n$, the required inequality is non-trivial and needs to be proven only for $n-\frac{(n-1)n(n+1)}{6}x^2 \ge -n$ or $x^2 \le \frac{12}{n^2-1}$ which means $x^2 \le \frac{3}{2}$ when $n \ge 3$ so definitely $|x| < \frac{\pi}{2}$ so $\cos x >0$.

Note that $\frac{\sin(n+1)x}{\sin x}-f(n+1,x)=(\frac{\sin(n)x}{\sin x}-f(n,x))\cos x-2\sin^2(\frac{x}{2})f(n,x)-2\sin^2(\frac{nx}{2})+\frac{n(n+1)}{2}x^2$

So assuming by induction $\frac{\sin(n)x}{\sin x}-f(n,x) \ge 0$ (starting at $n=2$ as $2x^2 \ge 3$ hence $\cos x>0$ when $n+1 \ge 3$ while the inequality is trivial otherwise as seen above) and noticing that $-2\sin^2(\frac{nx}{2}) \ge -\frac{n^2x^2}{2}$. while if $f(n,x) \ge 0$ then $f(n,x) \le n$ so in any case $-2\sin^2(\frac{x}{2})f(n,x) \ge -\frac{n}{2}x^2$, we get:

$\frac{\sin(n+1)x}{\sin x}-f(n+1,x) \ge 0$ and we are done!

Answer 4

Alternative solution:

Remark: $n - \frac{n(n^2-1)x^2}{6}$ is the second order Taylor approximation of $f(x) = \frac{\sin nx}{\sin x}$ around $x = 0$.

First, we give the following result. The proof is given later.

Fact 1: Let $n\ge 3$ be a positive integer and $x\in (0, \frac{\pi}{2})$. Then $\frac{\sin nx}{\sin x} \ge n - \frac{n(n^2-1)x^2}{6}$.

The remaining cases are easy to prove:

For $n=1$, clearly the inequality is true.

For $n=2$, the inequality is equivalent to $2\cos x - 2 + x^2\ge 0$ which is true.

For $n\ge 3$ and $x\in [\frac{\pi}{2}, \infty)$, we have $-n \ge n - \frac{n(n^2-1)x^2}{6}$. It is easy to prove that $-n \le \frac{\sin nx}{\sin x} \le n$ for $x\in \mathbb{R}$ (by math induction). The inequality is true.

$\phantom{2}$

Proof of Fact 1: The inequality is written as $$\frac{\sin n x}{nx} \ge \frac{\sin x}{x} - \frac{n^2-1}{6}x^2\cdot \frac{\sin x}{x}.$$

To proceed, we need the following results (Facts 2 through 3). Their proof is not hard and hence omitted.

Fact 2: $\frac{\sin y}{y} \ge \frac{-7y^2+60}{3y^2 + 60}$ for $y\in \mathbb{R}$. (Pade $(2,2)$ approximation)

Fact 3: $\frac{\sin y}{y} \le \frac{6}{6+y^2}$ for $y \in (0, \frac{\pi}{2})$. (Pade $(0,2)$ approximation)

By using Facts 2 and 3, it suffices to prove that $$\frac{-7n^2x^2+60}{3n^2x^2 + 60} \ge \frac{6}{6+x^2} - \frac{n^2-1}{6}x^2\cdot \frac{-7x^2+60}{3x^2 + 60}$$ or (after clearing the denominators) $$(-7x^4+18x^2+360)n^4+(7x^4-200x^2-1200)n^2+140x^2 \ge 0.$$ Since $-7x^4+18x^2+360 > 0$, we have \begin{align} &(-7x^4+18x^2+360)n^4+(7x^4-200x^2-1200)n^2+140x^2\\ \ge \ & (-7x^4+18x^2+360)n^2\cdot 3^2+(7x^4-200x^2-1200)n^2+140x^2\\ = \ & (-56x^4-38x^2+2040)n^2+140x^2\\ \ge \ & 0 \end{align} where we have used the fact that $-56x^4-38x^2+2040 > 0$. We are done.