3

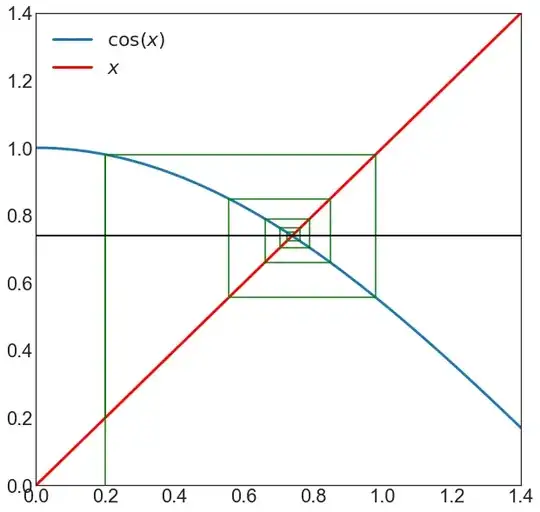
Let $f_{k+1}(x)=f_{k}(\cos x)$ and $f_{1}(x)=\cos x$ then $\lim_{k\to\infty}f_{k}(x)=0.73905\cdots$

I was just piddling around with the calculator one day. I don't know what happened but I just happened to take the cosine of a single number (in radians) repeatedly. It converged to a single value $0.739085133\dots$ It converged to this same thing for every number I tried. Like for example, the cosine of the cosine of the cosine of the cosine$\dots$ of any arbitrary value is equal to that.

Please tell me if I have made a new observation, or if it's just a false alarm.

jimjim
  • 9,675
thedamnedking17
  • 37
  • 1
    So basically you have been dabbling with the sequence $$ x_n = \cos{(x_{n-1})} $$ Which of course converges to a value of $x = \eta$ for which $$ \eta = \cos \eta $$ – Matti P. Apr 28 '20 at 11:54
  • 1
    It;s the unique fixed point of the cosine function, and it's an attracting fixed point. – Angina Seng Apr 28 '20 at 11:55
  • 1
    See also https://math.stackexchange.com/questions/1025806/computing-the-fixed-point-for-cos-x – Calvin Khor Apr 28 '20 at 12:04
  • the number doesn't need to be in radians , in can be in martian banana unit and the answer should be the same. – jimjim Apr 29 '20 at 08:57

2 Answers2

4

The function $f(x)=\cos (x))$ has just one fixed point ($x_0$ is a fixed point of $f(x_0)$ if and only if $f(x_0)=x_0$). That fixed point is as you found $x_0\approx 0.739085133$.

Then you can see that $|f'(x_0)|=|-\sin (x_0)|<1$.

So $x_0\approx 0.739085133$ is an attractive fixed point of $f(x)=\cos (x)$, and that's why you got that result using your calculator.

Alejandro Bergasa Alonso
  • 3,534
4

I know others have sufficiently answered your question, but I wanted to add a neat graphical representation. You can start from some particular $x$ value, go vertically to the $y=\cos(x)$ curve, then horizontally to the $y=x$ line, and repeat this process to zero in on the fixed point of $f(x)=\cos(x)$. fixed point of cosine

Here I'm starting with an initial $x$ value of $x_0=0.2$. Or alternatively, you can plot the function $f(x)=\cos\cos\cos...x$ for a large number of iterations and notice it is a nearly constant function. (I'll let you do this yourself.) As a final note this number is in fact transcendental and has a special name, the Dottie Number.

K.defaoite
  • 12,536