7

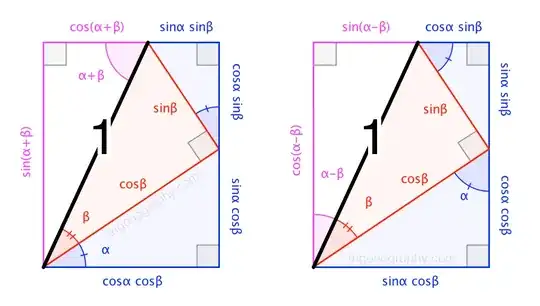
This is an exercise in Gelfand's Trigonometry, It is not that difficult but I am doing something wrong that is preventing me from proving the identity.

We need to use the following diagram to prove it: 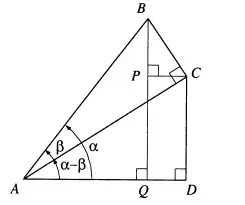enter image description here

My attempt:

$$ \begin{eqnarray*} \sin (\alpha - \beta) = \frac{CD}{AC} \\ = \frac{PQ}{AC} \\ = \frac{BQ - BP}{AC} \\ = \frac{BQ}{AC} - \frac{BP}{AC} \\ \end{eqnarray*} $$

Now in the following step we should use an intermediary to make this equal to the required identity, but for the first fraction I can't find anything rather than $AB$} $$ = \frac{BQ}{AB} \cdot \frac{AB}{AC} \\ $$ My problem here is I don't see how $\frac{AB}{AC}$ would simplify to $\cos \beta$ to me this seems like $\sec \beta$ How could this be fixed?

nomen
  • 2,707
dude076
  • 389
  • 1
    The reason this approach ($\frac{BQ}{AC} - \frac{BP}{AC}$) doesn't yield what you want, is because it will not yield what you want.. E.g. let $AB = 1$, then $BQ = \sin \alpha, AC = \cos \beta$, there is no way to make $ BQ / AC = BC \times AC $ – Calvin Lin Apr 29 '20 at 15:53
  • 1
    Note that for the other fraction, you get $$ \frac{BP}{AC} = \frac{BP}{BC}\cdot \frac{BC}{AC} = \cos(\alpha-\beta)\tan(\beta) $$So 1) both terms want you to multiply by $\cos\beta$ or $\cos^2\beta$ to get rid of denominators, and 2) you have probably taken a wrong turn somewhere. – Arthur Apr 29 '20 at 15:59
  • So it seems like my approach was wrong from the beginning. Perhaps you could provide me a hint for this one? I tried using $\sin (\alpha) = \sin([\alpha-\beta]+\beta)$, and solve the equation for $\sin(\alpha - \beta)$, but that wasn't useful either. – dude076 Apr 29 '20 at 16:05
  • An approach I have in mind is to use the fact that $\sin(\alpha - \beta) = \sin (\alpha + (-\beta)$, and take advantage of the sine function being odd. But that doesn't use the diagram in any way. – dude076 Apr 29 '20 at 16:09
  • 1
    The correct approach is to use areas. I'll try to post a solution within an hour. – J.G. Apr 29 '20 at 16:23
  • 2
    Please refer to this diagram provided by @Blue, it's my personal favorite:https://math.stackexchange.com/questions/1292/how-can-i-understand-and-prove-the-sum-and-difference-formulas-in-trigonometry/1342#1342 – Vasili Apr 29 '20 at 16:26
  • 1
    Areas? Interesting. I know how to prove it using the cosine law, Ptolemy's theorem, the famous constructive proof, and the one I mentioned above. I'm just struggling with this diagram. – dude076 Apr 29 '20 at 16:28
  • Does this answer your question? Deriving sine difference formula – MathematicianByMistake Apr 29 '20 at 16:41
  • My last comment may have given poor advice. I know how to use another diagram to the same end, but I've been unable to adapt the strategy to this one. I recommend @Vasya's solution instead, although the angles will need to be relabelled. – J.G. Apr 29 '20 at 17:25
  • 1
    @J.G. I'm still interested in seeing the proof by areas, I hope you can post it. – dude076 Apr 29 '20 at 19:35
  • @MathematicianByMistake Not really, but thanks for the effort nonetheless. – dude076 Apr 29 '20 at 19:36
  • 1
    @MathematicianByMistake I agree that technically this is a duplicate. However I think it would be a disservice to the community to close this copy because it’s clearly of such a higher quality. – gen-ℤ ready to perish Apr 29 '20 at 20:10
  • @gen-zreadytoperish Agreed. I retract the vote. – MathematicianByMistake Apr 29 '20 at 21:21

2 Answers2

2

This website has a lot of cool stuff about trigonometry.

https://trigonography.com/2015/09/28/angle-sum-and-difference-for-sine-and-cosine/ enter image description here

GDGDJKJ
  • 864
1

I don't know if you like this or not. Let $AC=1$. Then in $rt\Delta ACD$, $$ \sin(\alpha-\beta)=CD=PQ=BQ-BP.$$ In $rt\Delta ABC$, $AC=AB\cos\beta$ and hence $AB=\frac1{\cos\beta}, BC=\tan\beta.$ So in $rt\Delta ABQ$, $$BQ=AB\sin\alpha=\frac{\sin\alpha}{\cos\beta}.$$ Also in $rt\Delta BPC$, $\angle PBC=\alpha-\beta$ and hence $$ BP=BC\cos(\alpha-\beta)=\tan\beta\cos(\alpha-\beta). $$ So one has $$ \sin(\alpha-\beta)=\frac{\sin\alpha}{\cos\beta}-\tan\beta\cos(\alpha-\beta). \tag{1}$$ Similarly $$ \cos(\alpha-\beta)=\frac{\cos\alpha}{\cos\beta}+\tan\beta\sin(\alpha-\beta). \tag{2}$$ Putting (2) in (1), one has \begin{eqnarray} \sin(\alpha-\beta)&=&\frac{\sin\alpha}{\cos\beta}-\tan\beta\cos(\alpha-\beta)\\ &=&\frac{\sin\alpha}{\cos\beta}-\tan\beta\left(\frac{\cos\alpha}{\cos\beta}+\tan\beta\sin(\alpha-\beta)\right)\\ &=&\frac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos^2\beta}-\tan^2\beta\sin(\alpha-\beta) \end{eqnarray} or $$(1+\tan^2\beta)\sin(\alpha-\beta)=\frac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos^2\beta} $$ or $$ \sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta. $$

xpaul
  • 44,000
  • This is probably it. I avoided this approach since it doesn't duplicate Gelfand's method of proving the sum identity, but it looks like there's no way around. Thank you! – dude076 Apr 29 '20 at 19:34