Prove $\sum_{n\geq1}\frac{2^n (1-\cos\frac{x}{2^n})^2}{\sin\frac{x}{2^{n-1}}}=\tan\frac{x}{2}-\frac{x}{2}$

Question

How to prove for $|x|<\pi$:

• $\sum_{n\geq1}\frac{2(1-\cos(\frac{x}{2^n}))}{\sin(\frac{x}{2^{n-1}})}=\tan(\frac{x}{2})$
• $\sum_{n\geq1}\frac{2^n (1-\cos(\frac{x}{2^n}))^2}{\sin(\frac{x}{2^{n-1}})}=\tan(\frac{x}{2})-\frac{x}{2}$

Any help will be appreciated.

Answer 1

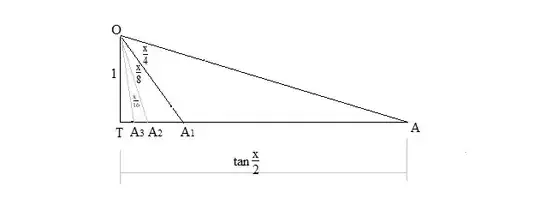
Here is a geometric proof for

$$\sum_{n\geq1}\frac{2(1-\cos\frac{x}{2^n})}{\sin\frac{x}{2^{n-1}}}=\tan\frac{x}{2}$$

Let $OA_1,\>OA_2,\>OA_3 …$ successively bisect the vextex angle $\angle O=\frac x2$ of the right triangle $OTA$, which leads to $\frac{AA_1}{TA_1} = \frac{OA}{OT}$, or,

$$AA_1= OA\cdot TA_1 = \sec\frac x2\tan\frac x4 = \frac{2\sin^2\frac x4}{\cos\frac x2\sin\frac x2} = \frac{2(1-\cos\frac x2)}{\sin x}$$

and, likewise,

$$A_1A_2 = \frac{2(1-\cos\frac x4)}{\sin \frac x2},\>\>\>\>\> A_2A_3 = \frac{2(1-\cos\frac x8)}{\sin \frac x4},\>\>\>\>\>A_3A_4 = ...$$

From the diagram, we have

$$\tan \frac x2 = AT = AA_1 + A_1A_2 + A_2A_3 + … = \sum_{n\geq1}\frac{2(1-\cos\frac{x}{2^n})}{\sin\frac{x}{2^{n-1}}}$$

Answer 2

Hint:

If $\sin4y\ne0,$

$$\dfrac{(1-\cos2y)^2}{\sin4y}=\dfrac{\sin^3y}{\cos y\cos2y}$$

$$=\dfrac{\sin y(1-\cos^2y)}{\cos y\cos2y}$$

$$=\dfrac{\sin(2y-y)}{\cos y\cos2y}-\dfrac{\tan2y}2$$ $$=\dfrac{\tan2y}2-\tan y$$

Set $2y=\dfrac x{2^n}$

$$\sum_{n=1}^\infty\dfrac{2^n\left(1-\cos\dfrac x{2^n}\right)^2}{\sin\dfrac x{2^{n-1}}}$$ $$=\sum_{n=1}^\infty2^n\left(\dfrac{\tan\dfrac x{2^n}}2-\tan\dfrac x{2^{n+1}}\right)$$

$$=\sum_{n=1}^\infty\left(f(n)-f(n+1)\right)\text{ (Telescoping series)}$$

$$=f(1)-\lim_{n\to\infty}f(n+1)$$

where $f(m)=2^{m-1}\tan\dfrac x{2^m}$

Now $$\lim_{n\to\infty}f(n+1)=\dfrac x2\cdot\lim_{n\to\infty}\dfrac{\tan\dfrac x{2^{n+1}}}{\dfrac x{2^{n+1}}}=?$$

Second part is much simpler

Set $2y=\dfrac x{2^n}$

$$\dfrac{1-\cos2y}{\sin4y}=\dfrac{2\sin^2y}{4\sin y\cos y\cos2y}=\dfrac{\sin(2y-y)}{2\cos y\cos2y}=?$$

Answer 3

Note

$$ \begin{align} (1-\cos\frac{x}{2^n})^2&= 1-2\cos\frac{x}{2^n} + \cos^2\frac{x}{2^n}\\ &=\sin^2\frac{x}{2^n}-2\cos\frac{x}{2^n}(1-\cos\frac{x}{2^n}) \\&=\sin^2\frac{x}{2^n}-4\cos\frac{x}{2^n}\sin^2\frac{x}{2^{n+1}} \end{align}$$

Then

$$\frac{(1-\cos\frac{x}{2^n})^2}{\sin\frac{x}{2^{n-1}}} = \frac{\sin^2\frac{x}{2^n} }{2\cos\frac{x}{2^{n}} \sin\frac{x}{2^{n}}} - \frac{4\cos\frac{x}{2^n}\sin^2\frac{x}{2^{n+1}}}{4\cos\frac{x}{2^{n}} \cos\frac{x}{2^{n+1}} \sin\frac{x}{2^{n+1}}} =\frac12\tan \frac{x}{2^n}- \tan\frac{x}{2^{n+1}} $$

Thus

\begin{align} \sum_{n\geq1}\frac{2^n (1-\cos(\frac{x}{2^n}))^2}{\sin(\frac{x}{2^{n-1}})} &= \sum_{n\geq1}\left( 2^{n-1} \tan \frac{x}{2^n}- 2^2\tan\frac{x}{2^{n+1}}\right) \\ &= \tan\frac{x}{2}-\frac{x}{2} \lim_{n\to \infty} \frac{\tan\frac{x}{2^{n+1}}}{\frac{x}{2^{n+1}}} = \tan\frac{x}2-\frac{x}{2} \end{align}