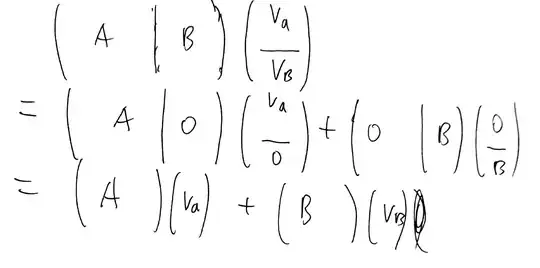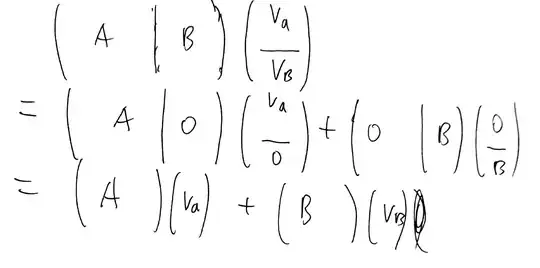Prove that $\dim(N(A|B)) = \dim(N(A)) + \dim(N(B)) + \dim(R(A) \cap R(B))$.

Question

Let $A$ be a $m \times n$ matrix and $B$ be a $m \times k$ matrix. Let $N(A),N(B),R(A),R(B)$ be the nullspace of $A$, the nullspace of $B$, the range of $A$, and the range of $B$, respectively. Prove that $$\dim(N(A|B)) = \dim(N(A)) + \dim(N(B)) + \dim(R(A) \cap R(B))$$

Any idea to solve it? Thanks for help in advanced.

what $N(A|B)$ denots ? – jacopoburelli May 02 '20 at 07:29 — jacopoburelli, May 02 '20 at 07:29
Idk, I guess it denotes the augmented matrix of both. – lap lapan May 02 '20 at 07:30 — lap lapan, May 02 '20 at 07:30

score 1 · Accepted Answer · answered May 02 '20 at 08:57

1

Whenever you see something like $\dim N(A)$, you know that “rank-nullity” is lurking.

What does this say in your case? You have three matrices, so you can say

$\dim R(A)+\dim N(A)=n$
$\dim R(B)+\dim N(B)=k$
$\dim R(A|B)+\dim N(A|B)=n+k$

Thus what you want to prove can be rewritten as $$ n+k-\dim R(A|B)=n-\dim R(A)+k-\dim R(B)+\dim\bigl(R(A)\cap R(B)\bigr) $$ which becomes $$ \dim R(A|B)=\dim R(A)+\dim R(B)-\dim\bigl(R(A)\cap R(B)\bigr) $$ Can you link $R(A|B)$ with $R(A)$ and $R(B)$ and apply another well-known result?

answered May 02 '20 at 08:57

egreg

238,574

i dont know how can $R(A|B) = R(A) + R(B)$ hold. – lap lapan May 02 '20 at 09:00
@arnold Just apply the definition: $R(A)$ is the subspace of $\mathbb{R}^m$ generated by the columns of $A$. – egreg May 02 '20 at 09:01
if I take $x \in R(A|B)$, what I can got? – lap lapan May 02 '20 at 09:01
so, $R(A|B)$ is the subspace of $\mathbb{R}^m$ generated by the columns of $A|B$? – lap lapan May 02 '20 at 09:04
@arnold Yes, so… – egreg May 02 '20 at 09:05
so, $R(A|B)$ is the subspace of $\mathbb{R}^m$ generated by columns of $A$ and $B$ ? – lap lapan May 02 '20 at 09:10
then, $R(A|B) = R(A) + R(B)$? – lap lapan May 02 '20 at 09:10
@arnold Yes, that's it. – egreg May 02 '20 at 09:15
Wow, great. I can feel the sense. Thanks! – lap lapan May 02 '20 at 09:16
So, from that, I can prove $dim(R(A|B)) = dim(R(A))+dim(R(B))-dim(R(A) \cap R(B))$? – lap lapan May 02 '20 at 09:17
@arnold Don't you know about Grassmann's formula? – egreg May 02 '20 at 09:30

Mira from Earth · Answer 2 · 2020-05-02T08:41:53.270

0

Treat $A,B, A|B$ as linear map form $R^n, R^k, R^{n+k}$ respectively to $R^m$.

By rank-nullity, the equality is

$(n+k)-dim(R(A|B)) = n-dim(R(A)) + k-dim(R(B)) + dim(R(A) \cap R(B))$

$dim(R(A|B)) = dim(R(A)) + dim(R(B)) - dim(R(A) \cap R(B))$

If we prove $R(A|B)=R(A)+R(B)$, the equality is equvalent to dimension fomula of $R(A)+R(B)$: $dim(R(A)+R(B)) = dim(R(A)) + dim(R(B)) - dim(R(A) \cap R(B))$

This formula is true, you can see:Dimension of the sum of two vector subspaces

Here is the rest of the proof($R(A|B)=R(A)+R(B)$):

For $x \in R(A)+R(B)$, there exist $v_a,v_b$ s.t. $x=Av_a+Bv_b$.

Let $v$ be (n+k)-vector with first n slots $v_a$ and last k slot $v_b$.

Then $x=(A|B)v \in R(A|B)$

Similarly, $x\in R(A|B)$, then $x=(A|B)v $ for some v.

Let $v_a$ be first n slots of v, $v_b$ be last k slots of v. Then $x=Av_a+Bv_b\in R(A)+R(B)$.

edited May 02 '20 at 08:41

answered May 02 '20 at 07:34

Mira from Earth

485

sorry, what is $n$ and $k$? – lap lapan May 02 '20 at 07:36
n, k are size of matrix you indicate – Mira from Earth May 02 '20 at 07:44
is $dim(R(A) \cap R(B))$ must be 0? – lap lapan May 02 '20 at 07:48
no it can be anything – Mira from Earth May 02 '20 at 07:51
but, why we only prove that $R(A|B)=R(A)+R(B)$ ? – lap lapan May 02 '20 at 07:54
I just edit a bit. They are both subspace of $R^m$. Then we can apply dimension fomula to prove – Mira from Earth May 02 '20 at 07:57
Let us continue this discussion in chat. – Mira from Earth May 02 '20 at 08:00
i still confusing on your proof – lap lapan May 02 '20 at 08:29
Which part then? – Mira from Earth May 02 '20 at 08:30
on the word "let v be (n+k)-vector..." and then – lap lapan May 02 '20 at 08:32
v is a vector with (n+k) slots, $v=(v_a^T|v_b^T)^T$ – Mira from Earth May 02 '20 at 08:35
what does $v_a$ and $v_b$ mean? – lap lapan May 02 '20 at 08:43
"For $x \in R(A)+R(B)$, there exist $v_a,v_b$ s.t. $x=Av_a+Bv_b$. " and "Let $v_a$ be first n slots of v, $v_b$ be last k slots of v. Then $x=Av_a+Bv_b\in R(A)+R(B)$. " I did define them, and first one exist by definition of rank space – Mira from Earth May 02 '20 at 08:49

Prove that $\dim(N(A|B)) = \dim(N(A)) + \dim(N(B)) + \dim(R(A) \cap R(B))$.

2 Answers2