Prove $\cos 20^\circ \cos 40^\circ \cos 80^\circ= \frac18$ geometrically

Question

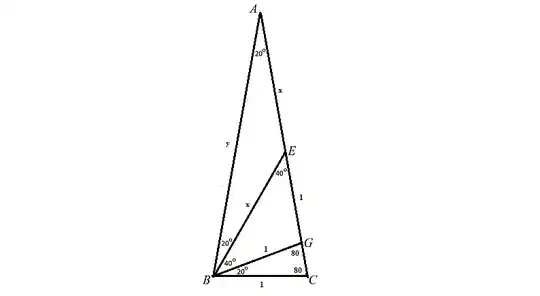
I understand the wizardry that $\cos 20^\circ \cos 40^\circ \cos 80^\circ=\dfrac18$

Proving it isn't that hard. Taking the left hand side and multiplying it up and down by $\sin 20$ yields:

\begin{align} & \dfrac{\sin 20^\circ}{\sin 20^\circ} \cdot \cos 20^\circ \cos 40^\circ \cos 80^\circ \\ =&\dfrac{\sin 40^\circ}{2\sin 20^\circ} \cdot \cos 40^\circ \cos 80^\circ \\ =& \dfrac{\sin 80^\circ}{4\sin 20^\circ} \cdot \cos 80^\circ \\ =& \dfrac{\sin 160^\circ}{8\sin 20^\circ}=\dfrac{\sin 20^\circ}{8\sin 20^\circ}=\boxed{\dfrac{1}{8}} \end{align}

My question is, is there a geometric proof of this, or the corollary $\sin 10 \sin 50 \sin 70^\circ$? Inspired by the possibility from this other indentity

I'm hoping that it's possible. I tried doing a similar construction as in the link that didn't go so well, mainly because of my repeated use of the cosine rule.

Is my quest achievable? Thanks for any guidance and advice.

Answer 1

Configure the relevant angles in the diagram and establish the followings

\begin{align} & \triangle ABE: \>\>\> \cos 20 = \frac{\frac y2}x = \frac y{2x}\\ & \triangle BGE: \>\>\> \cos 40 = \frac{\frac x2}1 = \frac x2\\ & \triangle ABC: \>\>\> \cos 80 = \frac{\frac12}y = \frac1{2y} \\ \end{align}

which lead to

$$\cos 20\cos 40 \cos 80 = \frac y{2x}\cdot\frac x2\cdot \frac1{2y} = \frac18$$