1

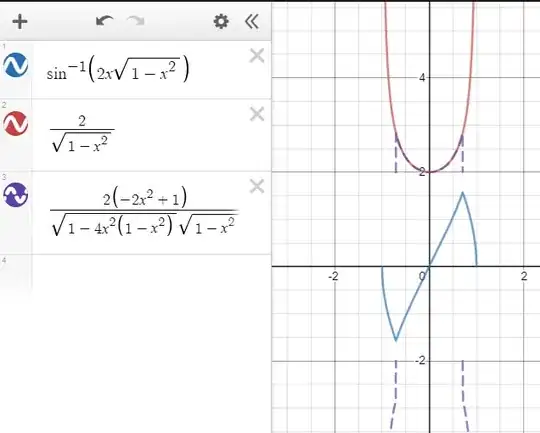
In our text book's(Higher Math 1st Paper-by S U Ahmed) differentiation chapter there is a section about replacing $x$(inside inverse trigonometric function) with trigonometric functions. A example problem was $\frac{d}{dx}\sin^{-1}\left(2x\sqrt{1-x^2}\right)$ and the solution given is;

Let \begin{align*} y &=\sin^{-1}\left(2x\sqrt{1-x^2}\right)\\ &= \sin^{-1}\left(2\sin \theta \sqrt{1-\sin^2 \theta}\right)\\ &=\sin^{-1}\left(2\sin \theta \cos \theta \right)\\ &=\sin^{-1}(\sin 2\theta )\\ &=2\theta\\ &=2 \sin^{-1}x \end{align*} Now, \begin{align*} \frac{d}{dx}\sin^{-1}\left(2x\sqrt{1-x^2}\right)&=\frac{d}{dx}2 \sin^{-1}x\\ &=\dfrac{2}{\sqrt{1-x^2}} \end{align*} But plotting two functions reveals the differentiation is not actually correct. If we differentiate by parts the answer would be $\frac{2\left(-2x^{2}+1\right)}{\sqrt{1-4x^{2}\left(1-x^{2}\right)}\sqrt{1-x^{2}}}$

[Plotted is Desmos1

Now my question is why this solution is wrong?

My guess: May be this is because replacing $x$ with $\sin \theta$ changes the range of $x$ from $(-\infty,\infty )$ to $[-1,1]$ and may be it causes some issue.

PinkyWay
  • 4,565
Soyeb Jim
  • 191
  • 3
    Set $y=x$ in https://math.stackexchange.com/questions/672575/proof-for-the-formula-of-sum-of-arcsine-functions-arcsin-x-arcsin-y – lab bhattacharjee Jun 13 '20 at 06:05
  • 1
    Because each of $\sqrt{1-\sin^2\theta}=\cos\theta$ and $\sin^{-1}(\sin 2\theta)=2\theta$ does not necessarily hold. Take $\theta=\frac{5\pi}{8}$. – mathlove Jun 14 '20 at 05:35

1 Answers1

0

Your guess is wrong. The range of x in original equation is [-1,1] to make the thing inside square root positive.

The problem starts when author writes sin^-1(sin(2theta)) = 2theta. This is wrong. Read about inverse trigonometry functions. The wrong thing is this is true for only some values of theta. For example, put theta = 60 degrees

Aditya Kumar
  • 36
  • the range of $x$ is $[-0.7071,0.7071]$ as the domain of $\sin\alpha$ is $[-1,1]$ so $2x\sqrt{1-x^}=[-1,1]$ – Soyeb Jim Jun 13 '20 at 06:42
  • 1
    Let f(x) = 2xsqrt(1-x^2). Then x=+-1/sqrt(2) is the point of local maxima where the value of f(x) gets 1 before and after which its value decreases. – Aditya Kumar Jun 13 '20 at 11:43