One missing step in proving $\mathbb{Z}\times \mathbb{Z} \cong \langle a,b\,|\, [a,b]=1\rangle$

Question

In order to understand the topic of "presentation of a group", I would like to work out the following example: $\def\Z{\mathbb{Z}} \def\iso{\cong} \def\llg{\langle} \def\rrg{\rangle}$

$\Z\times \Z \iso \langle a,b\,|\, [a,b]=1\rangle$, where $[a,b]:=a^{-1}b^{-1}ab$.

This example appears in Section 6.3 of Dummit and Foote's Abstract Algebra. The definition of generators and relations there is somehow confusing. It begins with a given group $G$ and a subset $S$ of $G$ such that $G=\llg S\rrg$ and then assume a subset $R$ of the free group $F(S)$ has the property that its normal closure in $F(S)$ equals to the kernel of the group homomorphism $\pi$, where $\pi$ is defined by the following commutative diagram:

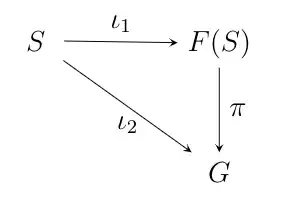
where $\iota_k$, $k=1,2$, are the inclusion maps. This a priori appearance of the group $G$ in the definition makes statements like the example above difficult to understand. To approach the example above, I will use the following definition instead:

Let $S$ be a set and $F(S)$ the free group on $S$. Let $R$ be a set of words in $F(S)$, i.e. $R\subset F(S)$, and $N$ the normal closure of $R$ in $F(S)$. The group $\llg S|R\rrg$ is defined as $$ \llg S|R\rrg=F(S)/N $$

Now let $S=\{a,b\}$, $\varphi(a)=(1,0)$, $\varphi(b)=(0,1)$. By the universal property of $F(S)$, there exists a unique group homomorphism $\pi: F(S)\to \Z\times\Z$ such that the following diagram commutes:

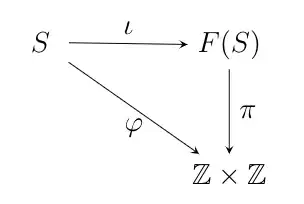
i.e., $\pi\circ\iota=\varphi$. If I can establish the following,

• $N=\ker\pi$;
• $\pi$ is surjective, (trivial because $\pi(a^mb^n)=m\pi(a)\oplus n\pi(b)$)

then by the first group isomorphism theorem, the proof is done.

The inclusion $\ker\pi\supset N$ is easy; since $\ker\pi$ is a normal subgroup, it suffices to show that $\ker\pi\supset R$: $$ \pi([a,b])=[\pi(a),\pi(b)]=[(1,0),(0,1)]=(0,0)\;. $$

How can I show the other direction $\ker\pi\subset N$? Or is there anything else I can do to get around this step?

Answer 1

I think the issue is your approach. I'm sure there is a way to show that $\text{ker}(\pi) \subseteq N$, but as you've noticed, it is quite hard to argue this directly. The combinatorics of words can be extremely complicated and it can be useful to avoid talking about them for "simple" problems like this.

It is for exactly this reason that "abstract nonsense" exists. You are already halfway there by using the universal property of the free group, why not go all the way and use the universal property of quotients?

To show $F(S)/N \cong \mathbb{Z}^2$, let's show that $\mathbb{Z}^2$ satisfies the universal property of the quotient! That is, let's show that

• for any hom $f : F(S) \to G$
• if $N \subseteq \text{ker}(f)$
• then $f$ descends to a unique hom $\tilde{f} : \mathbb{Z}^2 \to G$

So let's fix a map $f : F(S) \to G$, which satisfies $N \subseteq \text{ker}(f)$. That is, $f([a,b]) = [f(a),f(b)] = 1$.

But then we can set $\tilde{f}((1,0)) = f(a)$ and $\tilde{f}((0,1)) = f(b)$. If you know that $\mathbb{Z}^2$ is the free abelian group on two generators, then we're done. If not, then you should check by hand that this is actually a homomorphism which makes the quotient diagram commute. I'm sure you'll find this much easier than trying to show that $\text{ker}(\pi) = N$. If you find yourself wanting another hint, feel free to ask in a comment.

---

Edit:

To elaborate some, let's start with what the "universal property of the quotient" even means. The naming comes from a branch of math called Category Theory, and the idea is to characterize objects based on what morphisms they allow. You've already seen this in the Free Group, which has a universal property expressing what morphisms from the free group exist.

We can describe lots of different algebraic constructions in this way, including the quotient! The definition is as follows:

If $N \trianglelefteq G$, then a morphism $\pi : G \to K$ satisfies the universal property of the quotient (with respect to $G$ and $N$) if and only if: For every $f : G \to H$ with $N \subseteq \text{ker}(f)$, there is a (unique!) homomorphism $\tilde{f} : K \to H$ such that $f = \tilde{f} \circ \pi$.

Now I will leave it to you to show the following few facts, which will culminate in the theorem you want to prove:

1. Show $\pi : G \to G/N$ the natural quotient map satisfies the universal property of the quotient.

   • This says that the name is well chosen. Indeed, this is where the name comes from!

2. If two maps $\pi_1 : G \to K_1$ and $\pi_2 : G \to K_2$ both satisfy the universal property, then $\varphi : K_1 \cong K_2$, and moreover $\pi_2 = \pi_1 \circ \varphi$. So not only are $K_1$ and $K_2$ "the same", but so are the quotient maps $\pi_1$ and $\pi_2$.

   • If you haven't seen proofs like this before, this might take some ingenuity. As a hint, notice $\pi_2$ is a map out of $G$ with $N \subseteq \text{ker}(\pi_2)$. So since $K_1$ has the universal property, we must have a map $K_1 \to K_2$. Swapping the roles of $K_1$ and $K_2$, we also have a map $K_2 \to K_1$... Can you prove these maps compose to the identity?

3. Now can we show that $\mathbb{Z}^2$ satisfies the universal property with respect to $G = F(a,b)$ and $N = \langle [a,b] \rangle$?

   • This is what I outlined in the original part of the answer.

4. Finally, since $F(a,b)/N$ and $\mathbb{Z}^2$ both satisfy the universal property (by (1.) and (3.) respectively), conclude they must be isomorphic (by (2.)), which is what we're trying to show.

---

I hope this helps ^_^

Answer 2

In general, this kind of question is tricky. However, this specific example can be simplified if you are willing to use the fact that $\mathbb{Z\times Z}$ is the free abelian group on two generators.

We shall start with a "squishing" argument: the group defined by $\langle a, b\mid [a, b]=1\rangle$ maps onto $\mathbb{Z\times Z}$, and vice-versa.

Firstly, by the universal property of free groups, note that $\mathbb{Z\times Z}$ admits some presentation on two generators $\langle a, b\mid R\rangle$. As $\mathbb{Z\times Z}$ is abelian we have that $[a, b]=1$, and so $[a, b]\in N(R)$. This means that $\mathbb{Z\times Z}$ is a homomorphic image of the group with presentation $\langle a, b\mid [a, b]=1\rangle$.

On the other hand, the group with presentation $\langle a, b\mid [a, b]=1\rangle$ is abelian, and so, by the universal property of free abelian groups, it is mapped onto by $\mathbb{Z\times Z}$.

Hence, our "squishing" is complete, and (abusing notation by writing the presentation for the group defined by it) we have surjections $\phi_1$ and $\phi_2$ as follows: $$\mathbb{Z\times Z}\xrightarrow{\phi_1}\langle a, b\mid [a, b]=1\rangle\xrightarrow{\phi_2}\mathbb{Z\times Z}$$ Now, every proper quotient of $\mathbb{Z\times Z}$ contains elements of finite order (why?), and so either $\phi_2\phi_1$ is not surjective or has trivial kernel. As both maps are surjective their composition is surjective, and so $\phi_2\phi_1$ has trivial kernel. Therefore, $\phi_1$ is surjective and has trivial kernel, as required.

---

A similar argument can be used to define presentations of, for example, free nilpotent groups. However, the argument used the fact that the groups are Hopfian, which is not always the case. ("Hopficity" is what made the final paragraph tick - in general we can "squish" groups like above but not obtain an isomorphism.)