Integrate a weighted Bessel function over the unit disk

Question

I would like to evaluate a complex-valued integral of the form

$$ I_e = \int_0^1 x e^{iax} J_0(b \sqrt{1-x^2}) dx $$

where $a$ and $b$ are real numbers (not necessarily positive) and $J_0(z)$ is the Bessel function of the first kind.

An alternative statement of the problem can be considered by making a change of variables $z=b\sqrt{1-x^2}, c = a/b$, so that

$$ I_e = \frac{1}{b^2} \int_0^b z e^{ic\sqrt{b^2-z^2}} J_0(z) dz. $$

I am particularly interested in the special case of $0\leq b \leq 100$ with $c = 1$ or $-4 \leq c \leq -1$.

The task boils down to evaluating two real-valued integrals

$$ I_s = \frac{1}{b^2} \int_0^b z \sin(c\sqrt{b^2-z^2}) J_0(z) dz $$ $$ I_c = \frac{1}{b^2} \int_0^b z \cos(c\sqrt{b^2-z^2}) J_0(z) dz $$

The integral with the sine has a simple form given by Gradshteyn and Ryzhik (6.738.1) which, after simplification, becomes

$$ I_s = c \frac{j_1(b\sqrt{c^2 + 1})}{\sqrt{c^2 + 1}} = a \frac{j_1(\sqrt{a^2 + b^2})}{\sqrt{a^2 + b^2}} $$

where $j_1(z)$ is the spherical Bessel function of the first kind.

I am not exactly sure how this expression was derived. Perhaps it holds a clue. I tried substituting the integral form of the Bessel function and integrating analytically but did not get very far.

By symmetry, I naively expected the integral involving the cosine to be proportional to the spherical Bessel function of the second kind $y_1(z)$ (and thus, the complex-valued integral to be proportional to the spherical Hankel function of the second kind), but that does not appear to be the case.

$$ I_c \neq -c \frac{y_1(b\sqrt{c^2 + 1})}{\sqrt{c^2 + 1}} $$

Particularly, because of the cosine term inside the Bessel function,

$$ \lim_{b\to0} I_c \neq \lim_{b\to0} -c \frac{y_1(b\sqrt{c^2 + 1})}{\sqrt{c^2 + 1}}$$

A better approximation can be achieved by dropping the cosine part of the spherical Bessel

$$ I_c \approx c \frac{\sin(b\sqrt{c^2 + 1})}{b(c^2 + 1)} $$

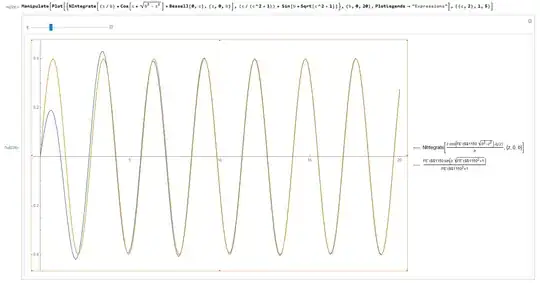
Indeed, if we plot $I_c \times b$, we can see that it is a regular sine wave for $b \geq 4$. My current goal is to find a correction term (via a series expansion, perhaps) that would improve the approximation for $b < 4$.

I've only found a single identity connected to the approximation given above. Tables of Integral Transforms, Vol. 2, p. 337, eq. 29 gives

$$ \int_0^b \frac{z}{\sqrt{b^2-z^2}} \cos(c\sqrt{b^2-z^2}) J_0(z) dz = \frac{\sin(b\sqrt{c^2 + 1})}{\sqrt{c^2 + 1}} $$

I am not sure what's the best way to connect this identity to $ I_c$. The two integrals only differ by the first term (and the constant $ 1/b^2$). One way is to perform a Taylor expansion around the origin:

$$\frac{z}{\sqrt{b^2-z^2}} = \frac{z}{b} + \frac{1}{2} \frac{z^3}{b^3} + O(z^5) $$

The left part is from the identity, and the first term on the right is from $I_c$. The cubic term does not appear to help, so perhaps this is not the right expansion to use in this case (and perhaps I should expand at infinity rather than at the origin).

I would appreciate any tips or guidance. Thank you!

Answer 1

For an evaluation of $I_s$, start with $$I_e = \int_0^1 x e^{iax} J_0(b \sqrt{1-x^2}) dx = \int_0^{\pi/2} \sin x \cos x e^{ia\cos x} J_0(b\sin x) dx$$ It is known that (proved easily by using series expansion of $J_\mu$ and beta function): $$J_{\nu+\mu+1}(z) = \frac{z^{\nu+1}}{2^\nu \Gamma(\nu+1)} \int_0^{\pi/2} J_\mu(z\sin x) \sin^{\mu+1}x \cos^{2\nu+1} x dx$$ Therefore taking imaginary part gives $$I_s = \sum\limits_{n = 0}^\infty {\frac{{{{( - 1)}^n}{a^{2n + 1}}}}{{(2n + 1)!}}{J_{n + 3/2}}(b)\frac{{{2^{n + 1/2}}\Gamma (n + 3/2)}}{{{b^{n + 3/2}}}}} = \sqrt {\frac{\pi }{2}} a\sum\limits_{n = 0}^\infty {\frac{{{{( - {a^2}/2)}^n}}}{{n!}}\frac{{{J_{n + 3/2}}(b)}}{{{b^{n + 3/2}}}}} $$ Now use equation $(1)$ proved in my answer here, we complete the proof: $$I_s = \sqrt {\frac{\pi }{2}} a\frac{{{J_{3/2}}(\sqrt {{a^2} + {b^2}} )}}{{{{({a^2} + {b^2})}^{3/4}}}}$$

---

Real part of $I_e$ gives $$I_c = \sum\limits_{n = 0}^\infty {\frac{{{{( - 1)}^n}{a^{2n}}}}{{(2n)!}}{J_{n + 1}}(b)\frac{{{2^n}n!}}{{{b^{n + 1}}}}} $$ I don't think this can be expressed in terms of Bessel-related functions only, but note that the summand decrease very rapidly (due to $n!/(2n)!$ and also $J_{n+1}(b)$), so this might be useful if you're interested in numerical calculations.