The number of real solutions of the equation $\cos(\cos(\cos(\cos(x)))) = \sin(\sin(\sin(\sin(x))))$

Question

The number of real solutions of the equation $$\cos(\cos(\cos(\cos(x)))) = \sin(\sin(\sin(\sin(x))))$$

(I have no clue to solve this problem)

Answer 1

\begin{align*} \cos(x) &\in [-1,1] \text{,} \\ \cos\cos(x) &\in [\cos(1),1] \text{,} \\ \cos\cos\cos(x) &\in [\cos\cos(1),\cos(1)] \text{, and} \\ \cos\cos\cos\cos(x) &\in [\cos\cos\cos(1),\cos\cos(1)] \text{.} \end{align*}

The second line is because cosine is even and attains its maximum, $1$ on the interval $[-1,1]$. We know $[\cos(1),1]$ only contains positive numbers (because $\cos(0) > 0$ and the least positive angle producing zero from the cosine is $\pi/2 > 1$).

\begin{align*} \sin(x) &\in [-1,1] \text{,} \\ \sin\sin(x) &\in [-\sin(1),\sin(1)] \text{,} \\ \sin\sin\sin(x) &\in [-\sin\sin(1),\sin\sin(1)] \text{, and } \\ \sin\sin\sin\sin(x) &\in [-\sin\sin\sin(1),\sin\sin\sin(1)] \text{.} \end{align*}

This last interval contains positive and negative numbers.

The only way there can be solutions is if the upper bound of the last interval for iterated sines is at least the lower bound of the last interval for iterated cosines. So, we must decide $$ \sin\sin\sin(1) \overset{?}{\geq} \cos\cos\cos(1) $$

One way to resolve this is with a calculator. \begin{align*} \sin\sin\sin(1) &= 0.6784304773607402289{\dots} \text{ and } \\ \cos\cos\cos(1) &= 0.6542897904977791499{\dots} \text{.} \end{align*} So the potential remains that there may be solutions. (And as observed in comments, by periodicity, there are either zero solutions or infinitely many.)

If $\sin(y)$ is going to be as large as the lower bound on the iterated cosines, it is at least as large as $1/2$. (This may seem like pulling a mysterious constant out of thin air; it is not. There are three angles in the first quadrant we are responsible for knowing very well. Their sines are $1/2$, $\sqrt{2}/2$, and $\sqrt{3}/2$. The other two are too large.) This requires $\pi/6 < y < 5\pi/6$ (up to an integer multiple of $2\pi$).

If $y = \sin(w)$, since $\pi/6 > 1/2$, the same argument requires $\pi/6 < w < 5\pi/6$ (up to an integer multiple of $2\pi$). (Now we have $\sin\sin(w) > 1/2$.)

If $w = \sin(z)$, since $\pi/6 > 1/2$, the same argument requires $\pi/6 < z < 5\pi/6$ (up to an integer multiple of $2\pi$). (Now we have $\sin\sin\sin(z) > 1/2$.)

Repeating the argument again, we find that for $\sin\sin\sin\sin(x) > 1/2$ it is the case that $\pi/6 < x < 5\pi/6$ (up to an integer multiple of $2\pi$). So any solution on $[0,2\pi]$ has $x \in [\pi/6, 5\pi/6]$.

For $x \in [\pi/6, 5\pi/6]$, \begin{align*} \cos(x) &\in [-1/2,1/2] \text{,} \\ &\vdots \\ \cos\cos\cos\cos(x) &\in [\cos\cos\cos(1/2),\cos\cos(1)] \\ &= [0.698{\dots}, 0.857{\dots}] \text{.} \end{align*}

So for the angles where the iterated sine is large enough to meet the range of the iterated cosine, the iterated cosine is greater than the maximum of the iterated sine. Therefore, there is no solution.

We can also see this from a plot of the two iterated functions.

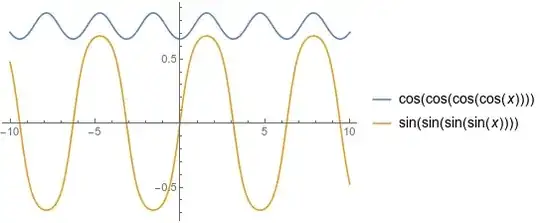
The upper bound of the orange trace is higher than the lower bound of the blue trace, but whenever the orange trace is $\geq 1/2$, the height of the blue trace is at least $0.698{\dots}$, which is above the upper bound of the orange trace ($0.678{\dots}$).