Can you compute the derivatives of $\sin^{-1}(x),\cos^{-1}(x),$ and $\tan^{-1}(x)$ using only geometry?
I know how to use geometry to find the derivatives of $\sin x$ and $\cos x$ like this:
We can use the fact that we know the tangent of the circle to show that $\frac{d}{dx}\cos(x)=\sin(x)$.
Wondering if you can do the same with the inverse functions.
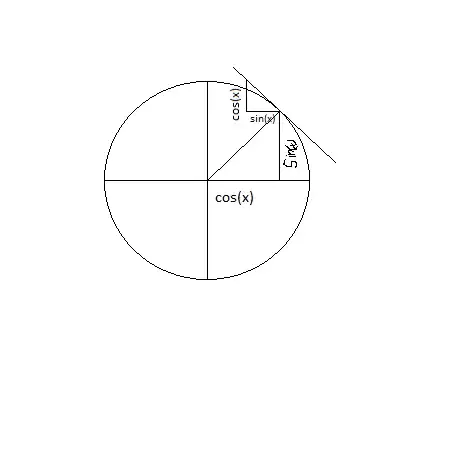
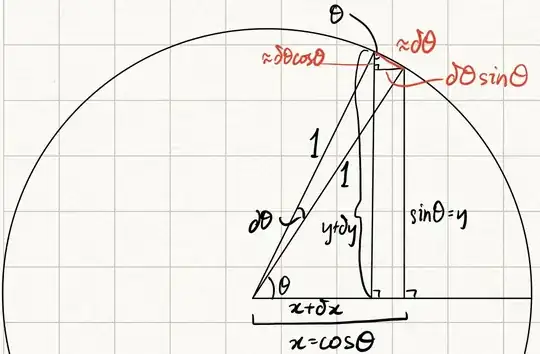
It is similar to the derivation of cos(x) or sin(x) geometrically.
Let $\theta_1 = \arcsin(x)$
$$\sin(\arcsin(x)) = x = P$$ $$\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))}= \sqrt{1-x^2}= B $$ $$H = 1$$
A very important result used in all the cases, $$\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1$$ And assume $$\lim_{x \rightarrow 0} {\sin x} = x$$
You wouldn't even need to use $\sin'(x) = \cos(x)$
Sorry for the bad drawing and not drawing a unit circle:(
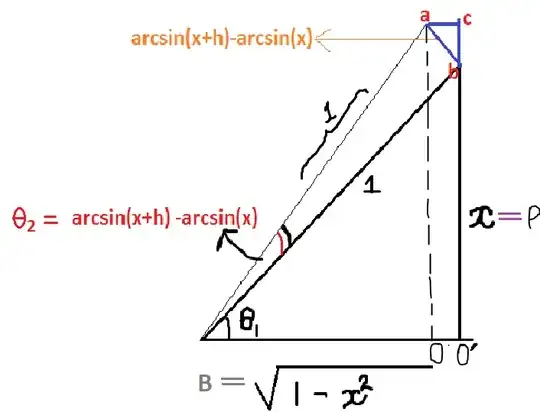
If carefully notice $$\theta_1 + \theta_2 = \arcsin(x+h)$$ As in other differential equations we will take $h \rightarrow 0$ at the end $$\theta_2 = \arcsin(x+h)-\arcsin(x)$$ $$AO' = \sin(\theta_1 + \theta_2)$$ $$AO' = \sin(\arcsin(x+h)) = x+h$$ $$CB = AO' - AO = x+h -x = h$$ $$AC = OO'$$ $$AC = \cos(\arcsin(x))-\cos(\arcsin(x+h) )$$ $$AC = \sqrt{1-x^2} - \sqrt{1-(x+h)^2}$$ $$AC = h \lim_{h\rightarrow 0}\frac{\sqrt{1-x^2} - \sqrt{1-(x+h)^2}}{h}$$ $$AC =- h \frac{d}{dx}(\sqrt{1-x^2})$$ Use Chain Rule $$AC = -h\frac{-x}{\sqrt{1-x^2}}$$ $$AC = h\frac{x}{\sqrt{1-x^2}}$$ Using Pythagoras Theorem for ABC
$$AB^2 = AC^2 + BC^2$$ $$AB^2 = h^2\frac{x^2}{ 1-x^2}+ h^2$$ $$AB = h\sqrt{\frac{x^2 +1-x^2}{1-x^2}}$$ $$AB = h\sqrt{\frac{ 1 }{1-x^2}}$$ $$AB = \sin(\theta_2)$$ $$AB = \lim_{h\rightarrow 0}\sin(\arcsin(x+h)-\arcsin(x) )= \lim_{\theta_2 \rightarrow 0}\sin(\theta_2)$$ $$AB = \theta_2$$ $$\theta_2 = h \frac{ 1 }{\sqrt{1-x^2}}$$ $$\theta_2/h = \frac{ 1 }{\sqrt{1-x^2}}$$ $$\lim_{h \rightarrow 0} \frac{\arcsin(x+h)-\arcsin(x)}{h} = \frac{ 1 }{\sqrt{1-x^2}}$$
Now you can do the same for $\arccos (x)$, but since this proof was done by only using $\sin(x)/x = 1$,
Let $\theta_2 = \arccos(x-h) - \arccos(x)$ You can also assume h to be positive but this is a lot easier
$B = x$
$P = \sqrt{1-x^2}$
$H= 1$
$$BC = \sqrt{1-(x-h)^2}- \sqrt{1-x^2}$$ $$BC^2 = h^2 \frac{x^2}{ {1-x^2}}$$ $$AC^2 = h^2$$ AB remains the same $$AB = \theta_2 = h \frac{ 1 }{\sqrt{1-x^2}}$$ $$\lim_{h \rightarrow 0} \frac{\arccos(x-h)-\arccos(x)}{h} = \frac{ 1 }{\sqrt{1-x^2}}$$ But....
$$\lim_{h \rightarrow 0} \frac{\arccos(x+h)-\arccos(x)}{h}= \lim_{h \rightarrow 0} \frac{\arccos(x-h)-\arccos(x)}{-h}$$
$$\frac{\mathsf d}{\mathsf {dx}}(\arccos(x)) = -\frac{ 1 }{\sqrt{1-x^2}}$$
I found out that arctan also requires a similar approach
https://en.wikipedia.org/wiki/Inverse_trigonometric_functions
Given that $\theta = \arcsin y,$ by looking at the picture, we have $$\theta + \delta \theta = \arcsin (y + \underbrace{\delta \theta \cos \theta}_{=\delta y})$$
Hence, $\delta y = \delta \theta \cos \theta$. Recalling that $\cos \theta = \sqrt{1 - \sin^2 \theta } = \sqrt{1 - y^2},$ we have
$$\boxed{\delta \arcsin y = \frac{1}{\sqrt{1 - y^2}}\delta y}.$$
Similarly, we can see that $\delta x = - \delta \theta \sin \theta$, so we get the corresponding result:
$$\boxed{\delta \arccos x = - \frac{1}{\sqrt{1 - x^2}}\delta x}.$$
