4

I asked this a while ago: For more background information.... Not required for this question...

2020/07/24 - changes at end

  • I have a vector, it contains 3 curvatures.
  • A curvature is a change in angle over time, it is either an unit circle/sphere arc-length or angle.
  • because this is purely about curvature, 'axis' will often be referred to as 'axle', since each component represents the curvature of the perpendicular plane around the axle.
  • The sum of the absolute value of the 3 components is the total curvature. (divided by 2 somewhere)
  • For a specific (X,Y,Z) vector there is a specific orientation; this can be demonstrated using the Show Basis Map or Show Inverse Basis Map options.

$$\begin{matrix}theta= (|X|+|Y|+|Z|)/2 * d_T\\ q_r = cos(theta)\\ q_i = sin(theta) * X / \sqrt(XX+YY+ZZ)\\ q_j = sin(theta) * Y / \sqrt(XX+YY+ZZ)\\ q_k = sin(theta) * Z / \sqrt(XX+YY+ZZ)\end{matrix}$$

\begin{bmatrix}1-2q_{j}^{2}-2q_{k}^{2}&2(q_{i}q_{j}-q_{k}q_{r})&2(q_{i}q_{k}+q_{j}q_{r})\\2(q_{i}q_{j}+q_{k}q_{r})&1-2q_{i}^{2}-2q_{k}^{2}&2(q_{j}q_{k}-q_{i}q_{r})\\2(q_{i}q_{k}-q_{j}q_{r})&2(q_{j}q_{k}+q_{i}q_{r})&1-2q_{i}^{2}-2q_{j}^{2}\end{bmatrix} $$ up = 2(q_iq_j-q_kq_r, 1/2-q_i^2-q_k^2, q_jq_k+q_iq_r) $$

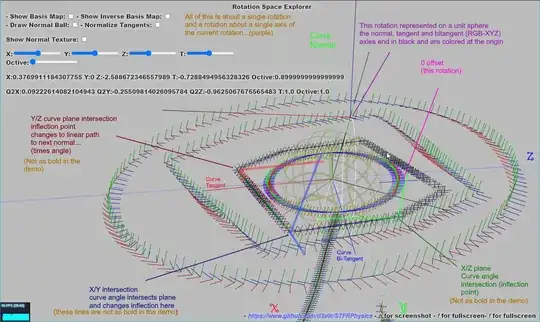
  • For a specific ($X$,$Y$,$Z$) vector there is a curve of related ($X_n$,$Y_n$,$Z_n$) curvatures that share the same normal. This demonstration is just showing the curve of rotation vectors that share the same normal as some specified input (controlled by the X, T, and Z sliders; T is the y rotation... the existing Y slider controls the target rotation; which is the destination point around the curve)

  • The curve is formed by linear interpolation from the intersection points where the unit circle centered at the origin, and the normal of the curve of rotations that share the same normal(up/green) : $((X,Y,Z)/\sqrt(XX+YY+ZZ)) × up(d_T=1/2)$. This substitution results in a double-angle sin/cos substitution, so the /2 of the normal is not used; but IS used anyway because of the 0.5 dT scalar... (represented with *0.5 instead of /2 )

    • $ x = { X \over \sqrt(XX+YY+ZZ) }$, $ y = { X \over \sqrt(XX+YY+ZZ) } $, $ z = { X \over \sqrt(XX+YY+ZZ) } $, $ t = { |X|+|Y|+|Z| } * 0.5 $
    • $ curve_{up_x} = {z * ( 1 - ( 1/2 - \cos(t) ) ( zz - xx - yy ) ) - \sin(t) * yx } $ $ curve_{up_y} = { \sin(t) * ( xx - zz ) } $ $ curve_{up_z} = { x * ( 1 - ( 1/2 - \cos(t) ) ( zz - xx - yy ) ) - \sin(t) * yz }$
    • (untested; algebraic substitution)

  • the tangent(right/red) is : $up(d_T=1/2)$

  • the bi-tangent(forward/blue) is : $normal × tangent$

  • These are the plane crossings where the slope changes from one crossing to the next... There are a maximum of 6 plane crossings and a minimum of 4, if the curve lies exactly in a plane (has a 0 curvature component for that axle). The x y and z plane intersections are... ( $plane_{coordinate}$ )

    $x_x=0$; $x_y =2* -curve_{up_z}/(|curve_{up_y}|+| curve_{up_z}|)$; $x_z =2* curve_{up_y}/(|curve_{up_y}|+ |curve_{up_z}|)$

    $y_x =2* curve_{up_z}/(|curve_{up_z}|+|curve_{up_x}|)$; $y_y=0$; $ y_z = 2* -curve_{up_x}/(|curve_{up_z}|+|curve_{up_x}|)$

    $z_x =2* -curve_{up_y}/(|curve_{up_x}|+| curve_{up_y}|)$; $z_y =2* curve_{up_x}/(|curve_{up_x}|+|curve_{up_y}|)$; $z_z=0$

    • These can also be computed for the square normal - that lies in the circle formation instead of the linear; though I expect updating the unit X,Y and Z components will be easier with a linear adder.

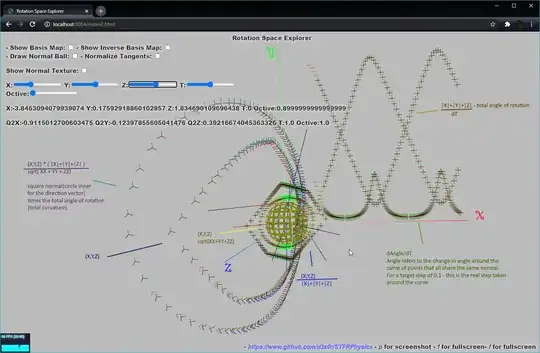
  • (A) For each step around the curve, there is a certain total rotation of that system, this is shown as a graph on the X/Y plane that has a characteristic sin/cos wave to it, and the max+min rotation is always 2π. The scalar of this curve is a component I miss. $ Y = |X|+|Y|+|Z|, X = T $

  • (B) for each step, the angle around the curve changes by a varying amount, this is shown on the X/Y plane, and shows the angle change per step of unit angle around the curve; this $d_{Angle}/d_T$ is one component I miss. This curve is created with the normal of the rotation... $acos(Rotation_t · Rotation_{t-1} )$ as $t$ steps around the curve.

Question - what are the functions that generate (A) and (B); right now all I have is a plot, and all the numbers that went into generating those points on the curve.

Reason for the question; Given any arbitrary axis of rotation, these functions will generate the angle-angle-angle updates without translating to a matrix and making assumptions about the reverse translation.

Additional Notes: There are distinct intervals or 'octaves' which for a spin of -2pi to 2π, 2π to 6π, -6pi to -2pi, etc... the relative rotations to stay within that octave are themselves distinct curves... There is a separate sort of calculation to reduce or increase curvature from one octave to another....

This is an overview. The axles are labeled with their color in script font X,Y,Z.

There is a graph (labeled in gold), which is the total sum of the rotation vector: Question part 1) What parameters define this curve? There is another graph (labeled in olive/green), which is the angle step around the curve for each step of twist: Question part 2 ) what parameters define this curve?

Explainer 1 enter image description here https://d3x0r.github.io/STFRPhysics/3d/index2.html https://github.com/d3x0r/STFRPhysics/blob/master/3d_index2_html.png (explainer 1) https://github.com/d3x0r/STFRPhysics/blob/master/3d_index2_html-2.png (explainer 2)

Edit:

  • Added options to enable/disable single curves, I realized others will not be as familiar with the character of a curve to be able to immediately identify it.
  • Reverse tangent and bi-tangent colors; looking at the graph, because Three.JS is reversed, and is left-handed, the 'right' should always appear 'left' which means the blue and red previously defined for the forward/right of the rotation curve were backwards. (attached images still are incorrect)
  • Modified cross product of rotation with up(1/2); it should be the square-normal of the coordinates

2020/07/24

Partial Rodriguez Implementation

Inputs to this are $yaw_{angle}$, $rotation_{axis}$, and a q which has {x,y,z} as the primary values and the following partial products.. {nx,ny,nz} as the normalized spin values (square axis of rotation), {nL} which is the linear normal or |x|+|y|+|z|, {nR} which is the square normal or sqrt(xx+yy+zz), {qw,s} are the cos/sin of nL/2 (qw represents the exp() partial result... converting from log-quaternion to quaternion sets w of the quaternion as cos(theta/2), so qw is the pre-computed quaternion partial w); and as a side note - the 'w' part of rotation log-quaterions is always 0 (again, exp(0)=1 ).

Was reading https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation#The_composition_of_spatial_rotations and saw $$\cos\frac{\gamma}{2} = \cos\frac{\beta}{2}\cos\frac{\alpha}{2} - \sin\frac{\beta}{2}\sin\frac{\alpha}{2} \mathbf{B}\cdot \mathbf{A}$$ which, before that goes a step too far, is just perfect. This is a very long expression: $$cos_{over2} = \cos(|x|+|y|+|z|/2) * \cos(yaw_{angle}/2) + \sin(|x|+|y|+|z|/2) * \sin(yaw_{angle}/2) * (x*basis_{up_x}+y*basis_{up_y}+z*basis_{up_y})$$ And then compute the result angle... $$result_{angle} = 2*arccos( cos_{over2} )$$ the Dot Product is also the cos(angle between axles of rotation). Basis up can be retrieved from above matrix. [ax,ay,az] is the normalized, axis of rotation to rotate around.

$$\begin{matrix} [ax,ay,az] = ||rotation_{axis}||\\ as = sin(yaw_{angle})\\ ac = cos(yaw_{angle})\\ q.s = sin( original_{angle})\\ q.qw=cos(original_{angle}) \end{matrix} $$

$$ \begin{matrix} Cx = as * q.qw * ax + q.s * ac * q.nx + q.s*as*(ay*q.nz-az*q.ny)\\ Cy = as * q.qw * ay + q.s * ac * q.ny + q.s*as*(az*q.nx-ax*q.nz)\\ Cz = as * q.qw * az + q.s * ac * q.nz + q.s*as*(ax*q.ny-ay*q.nx)\\ sin_{angle} = \sin(result_{angle}/2) \\ C_{norm} = sin_{angle}*(|Cx/sin_{angle}|+|Cy/sin_{angle}|+|Cz/sin_{angle}|);\\ result_{x_{Angle}} = Cx/C_{norm}*result_{angle}\\ result_{y_{Angle}} = Cy/C_{norm}*result_{angle}\\ result_{z_{Angle}} = Cz/C_{norm}*result_{angle} \end{matrix} $$

The remaining results can be delay computed later from the above result values, however, these values are already just laying around from the above computation anyway...

$$\begin{matrix} result_{normal_x} = Cx/sin_{angle}\\ result_{normal_y} = Cy/sin_{angle}\\ result_{normal_z} = Cz/sin_{angle} \\ result_{normal_{linear}} = result_{angle}/2\\ result_{normal_{rect}} = sin_{angle}/C_{norm}*result_{angle}\\ result_{qw} = cos_{over2}\\ result_{s} = sin_{angle} \\ \end{matrix} $$

Using this transformation, any arbitrary axle can be specified, the axis can have the log-quaternion applied to put the axle relative to the rotation, and then use, or the axles to rotate around can be gotten from any log-quaternion basis for roll, pitch and yaw operation. Any of these axles of rotation have a smooth curve in rotation space which is their (square normal(result_n?) * total angle (|x|+|y|+|z|) ).

I expect the parameters of curvature is like the derivative of the above; which I probably don't need now that the rotations result in at least a good coverage of the rotation space naturally.

This error correction code can apply, so the result, which resembles( arccos(cos(a+b)) which should be approximately a+b, if the result angle is far from the input angles, attempt to correct the octave.

    let fix = ( result_angle - (q.nL+yaw_angle))
    // - result_angle is always -π to π
    // - q.nL is always positive (the individual x/y/z signs determine directions)
    // - yaw_angle is often small, but may be positive or negative...
    //
    // this correction USUALLY just increments the angle to match the 
    // lnQ's octave, but the yaw_angle may change octaves...
    while( fix < -Math.PI*4 ){
        ang += Math.PI*4;
        fix += Math.PI*4;
    }
    while( fix > Math.PI*4 ){
        ang -= Math.PI*4;
        fix -= Math.PI*4;
    }
J Decker
  • 111
  • 4

0 Answers0