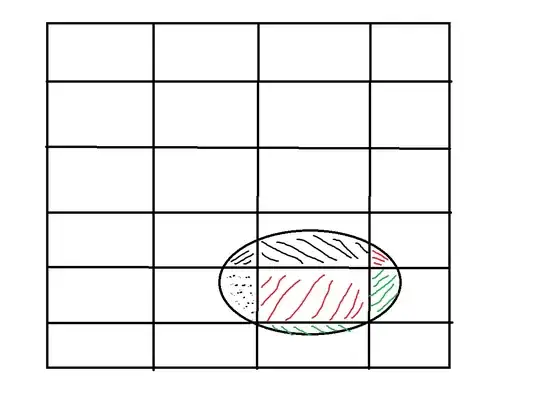
There is a trick here:
Your ellipse isn't slanted at all. It is perfectly straight, with center at $(0,0)$, the $x$-axis as major axis, and the $y$-axis as minor axis. In fact, it isn't even eccentric. It's a circle. It is your grid that is slanted and off-center, and squished or stretched. Why? Because slanted lines and circles are much easier to deal with than straight lines and slanted ellipses.
Suppose in grid coordinates your ellipse is centered at $(c_x, c_y)$, has major and minor semi-axes of $a$ and $b$ respectively, and has its major axis at an angle $\theta$ counterclockwise from the positive $x$-axis. And suppose the vertical grid lines have equations $x = \hat x_k$ and the horizontal grid lines have equations $y = \hat y_k$.
We can represent these lines as parametric vector functions:
$$\vec v(t) = \hat x_k\mathbf i + t\mathbf j\\\vec h(t) = t\mathbf i + \hat y_k\mathbf j$$
where $\mathbf i = (1, 0)$ and $\mathbf j = (0,1)$ in grid coordinates.
We perform the transformation in three stages:
- First, move the origin to the center of the ellipse. This just replaces $\hat x_k, \hat y_k$ with $$x_k = \hat x_k - c_x\\y_k = \hat y_k - c_y$$ As vectors, $\mathbf i$ and $\mathbf j$ are unaffected by this translation.
- Second, we rotate the coordinate system counterclockwise by $\theta$. This has the effect of rotating the coordinate representations of vector clockwise by $\theta$. In the new coordinate system, the two vectors become
$$\mathbf i = (\cos\theta, -\sin\theta)\\\mathbf j = (\sin\theta, \cos\theta)$$
- Scale $x$-coordinates by $a$ and $y$-coordinates by $b$. Now the vectors are $$\mathbf i = \left(\frac{\cos\theta}a, -\frac{\sin\theta}b\right)\\\mathbf j = \left(\frac{\sin\theta}a, \frac{\cos\theta}b\right)$$
Now you may have an objection here. That last transformation changed all the areas, and those are what you were trying to find. This is true, but the change is proportional: all areas are scaled by a factor of $\dfrac1{ab}$. In particular, the original ellipse has area $\pi ab$, while the transformed ellipse is a unit circle of area $\pi$. Once you calculate the areas in this system, you can get the corrsponding areas in grid coordinates by multiplying by $ab$.
Now that the problem is transformed, the issues mentioned in the comments become much smaller. Your gridlines are still given by $$\vec v(t) = x_k\mathbf i + t\mathbf j\\\vec h(t) = t\mathbf i + y_k\mathbf j$$
though now the vectors $\mathbf i, \mathbf j$ are no longer unital or orthogonal. Such a line will intersect the circle if and only if its closest approach to the origin is within a distance of $1$. That closest approach occurs when the position vector $\vec v_0$ is perpendicular to the direction of the line. I.e.
$$\vec v(t) \cdot \mathbf j = 0\\x_k \mathbf i\cdot \mathbf j + t \mathbf j\cdot \mathbf j = 0\\t = -x_k \dfrac{\mathbf i\cdot \mathbf j}{\mathbf j\cdot \mathbf j}
\\\vec v_0 = x_k\left(\mathbf i - \dfrac{\mathbf i\cdot \mathbf j}{\mathbf j\cdot \mathbf j}\mathbf j\right)$$
and similarly for the originally horizontal lines, the point of closest approach is
$$\vec h_0 = y_k\left(\mathbf j - \dfrac{\mathbf i\cdot \mathbf j}{\mathbf i\cdot \mathbf i}\mathbf i\right)$$
The gridlines for which $\|\vec v_0\|^2 < 1$ or $\|\vec h_0\|^2 <1$ are those that intersect the circle. The others are outside (or at best, tangent to the circle).
There are several possible approaches to calculating the areas these lines cut the circle into. One way is to find all points of intersection between the gridlines and the circle, which amounts to solving $\|\vec v(t)\|^2 = 1, \|\vec h(t)\|^2 = 1$ for the intersecting grid lines, which will be quadratic equations in $t$. Once you've identified the points, you can use the atan2 function to convert them to angles $\phi_i$ from the positive $x$-axis. These angles break the circle into sectors, whose central angle is the difference $\alpha = \phi_{i+1} - \phi_i$ between adjacent angles. The arcs of these sectors all lie within a single cell (since moving from one cell to another means intersecting a gridline). Since cells are convex, if we draw the chord for each arc, that chord must also lie within the same cell, as well as the region between them. The area of this sliver is $\frac 12\left(\alpha - \sin\alpha\right)$.
The region inside these chords is polygonal, and so are the intersections of the various cells with that polygon. Determine those cell-intersection polygons for each cell and calculate its area with the algorithm of your choice. Add in the areas of the slivers to the cells where they lie. Multiply by $ab$ to convert to the original picture and you are done.
While there are some programming challenges in finding the polygonal intersections, these are issues that have been solved before.
This picture shows the situation I described.
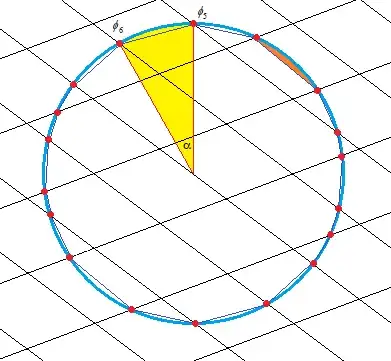
A sector is a region such as the one colored yellow, comprising of the area inside the circle and between two radii. By the "central angle" I meant the angle $\alpha$ formed by the two radii.
If $\phi_5 = \operatorname{atan2}(x_5, y_5), \phi_6 = \operatorname{atan2}(x_6, y_6)$ are the angles from the positive $x$-axis for the two intersection points, then $\alpha = \phi_6 - \phi_5$. Since the circle has radius $1$, when measured in radians, $\alpha$ is also the length of the circular arc between the two intersection points. And $\frac \alpha 2$ is the area of the sector.
The dark blue lines connecting the intersection points are the chords. There is one chord for each sector formed by the intersections. The chord and the two radii form a triangle whose area is $\frac 12\sin\alpha$, which makes the area of the sliver (the region between the chord and the circular arc, such as the one for a different sector I colored orange - there is a name for it, but I don't recall) to be $$\frac \alpha 2 - \frac 12\sin\alpha = \frac 12\left(\alpha - \sin\alpha\right)$$
For each of the cells intersecting the circle, the area inside the circle will be the sum of the sliver area, and the area of the polygon formed by the chord and the parts of the cell walls lying within the circle.
To find the area of a polygon with $n$ sides, take the sequence of its vertices $\{p_i\}_{i=1}^n$ in counter-clockwise order, and let $p_0 = p_n$. If $p_i = (x_i, y_i)$, then
$$\text{Area} = \frac 12\sum_{i=1}^n (x_{i-1}y_i - x_iy_{i-1})$$
(As long as your cell sizes are roughly on the same order as your ellipse size, you can use that formula naively. If your cells are hundreds or thousands of times smaller than your circle, then you might need to restructure it a bit to avoid cancellation error becoming significant.)