Prove $\cos^2(\theta)+\sin^2(\theta) = 1$

Question

$$\cos^2(\theta) + \sin^2(\theta) = 1$$

I solved this by using right triangle,

$$\sin(\theta) = \frac{a}{c}, \quad \cos(\theta) = \frac{b}{c}$$

$$\cos^2(\theta) + \sin^2(\theta) = 1$$

$$\Bigl(\frac{b}{c}\Bigr)^2 + \Bigl(\frac{a}{c}\Bigr)^2 = 1 $$

$$\frac {a^2 + b^2} {c^2} = 1 $$

now using Pythagorean identity: $a^2 + b^2 = c^2$

$$\frac {c^2} {c^2} = 1, \quad 1 = 1 $$

Answer 1

You solved this by using some right triangle but there isn't a right triangle in your solution? Remember, things like that have to be explicitly written in your proof.

Also, the proof is not very valid because you started off by asserting that:

$$\sin^2(\theta)+\cos^2(\theta) = 1$$

when really, what you should have started with is just the left-hand side of that. In other words, I can see where you're going with the reasoning but it isn't airtight because of your wording.

Really, what you should have done is to say that:

$$\sin(\theta) = \frac{a}{c}$$

$$\cos(\theta) = \frac{b}{c}$$

where $a,b,c$ are the sides of a particular right triangle whose image you're supposed to include. Then, you have:

$$\sin^2(\theta)+\cos^2(\theta) = \frac{a^2}{c^2} + \frac{b^2}{c^2} = \frac{a^2+b^2}{c^2}$$

By Pythagoras's Theorem relating the sides of the right triangle, it is the case that $a^2+b^2 = c^2$. Hence, we have:

$$\sin^2(\theta) + \cos^2(\theta) = \frac{a^2+b^2}{c^2} = \frac{c^2}{c^2} = 1$$

which proves the desired result.

Answer 2

My start, for my students is the real circunference $\mathcal C$ of center $O(0,0)$ and radius $r$, $P\equiv(x,y)\in \mathcal C$ $$\mathcal C\colon \quad x^2+y^2=r^2$$ $r>0$ and $x=r\cos\theta, y=r\sin\theta$, $\theta\in[0,2\pi[$, that it gives: $$r^2\cos^2\theta+r^2\sin^2\theta=r^2 \iff r^2(\cos^2\theta+\sin^2\theta)=r^2$$ Hence dividing by $r^2>0$ you have:

$$\cos^2\theta+\sin^2\theta=1$$

Answer 3

The asker seems to have the basic idea of the argument down. However, this question is tagged solution-verification, thus I believe that the asker wants feedback on their argument. Other answers have provided alternative proofs of this results, but these seems not to really address the question of critiquing the proof or its presentation.

Definitions

The argument that you give is a little unclear, as you have not unambiguously defined the objects you are working with, nor how they are meant to fit together. In American high schools, the definitions given for trigonometric functions are usually in terms of right triangles, e.g. $\sin(\theta) = \text{opp}/\text{hyp}$, where $\text{opp}$ is the length of the side oppose the angle $\theta$ in a right triangle, and $\text{hyp}$ is the length of the hypotenuse of that triangle.

However, this is not the only way to define trigonometric functions. In other contexts, the trigonometric functions might be defined in terms of points on the unit circle, or as the solutions to certain differential equations, or by their Taylor series, or in terms of the complex exponential function, and so on.

I cannot emphasize this enough: definitions matter! Everything in mathematics comes down to applying arguments to well defined mathematical objects. Often, a single mathematical object can be defined in multiple (equivalent) ways. Proving results about these objects depends on a thorough understanding their definitions.

Logical Structure

The argument you give is also a little unclear as you don't indicate which statements follow from the others. For example, when you write

$\cos^2(\theta) + \sin^2(\theta) = 1$

$(\frac{b}{c})^2 + (\frac{a}{c})^2 = 1 $

what does this mean? Does the first line imply the second? Does the second imply the first? Are the two statements entirely unrelated? You should connect the ideas in some manner, either using English or notation.

Moreover, as I read your argument, you start by assuming the conclusion. This is no good. You need to start with a known true statement, then show how that implies the desired statement. Again, it is helpful to be careful about indicating how one statement relates to the next.

Grammatical Structure

Good mathematical writing should be easy to read, in the sense that you should be able to read it out loud, and it should make sense. For example, you ought to write in complete sentences, mixing in notation only when it makes it easier to understand what is going on.

With the above in mind, here is how I would present your proof:

---

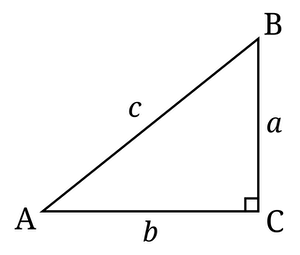
Definition: Let $\triangle ABC$ be an arbitrary right triangle, where $C$ is the right angle. Let $a$, $b$, and $c$ denote the lengths of the sides opposite the angles $A$, $B$, and $C$, respectively (see the image, above, taken from Wikipedia). Define the sine and cosine of the angle $A$ by $$ \sin(A) = \frac{a}{c} \qquad\text{and}\qquad \cos(A) = \frac{b}{c}. $$

Proposition: If $0 < \theta < 90^{\circ}$, then $ \sin(\theta)^2 + \cos(\theta)^2 = 1$.

Proof: Using the notation in the definition above, set $\theta = A$.^[1] Starting on the left-hand side of the desired identity, the definitions of sine and cosine give $$ \sin(\theta)^2 + \cos(\theta)^2 = \left(\frac{a}{c} \right)^2 + \left( \frac{b}{c} \right)^2. $$ Expand this and simplify to get $$ \left(\frac{a}{c} \right)^2 + \left( \frac{b}{c} \right)^2 = \frac{a^2}{c^2} + \frac{b^2}{c^2} = \frac{a^2 + b^2}{c^2}. $$ The Pythagorean theorem^[2] implies that $a^2 + b^2 = c^2$, and so $$ \frac{a^2 + b^2}{c^2} = \frac{c^2}{c^2} = 1. $$ Combining these equalities gives $$ \sin(\theta)^2 + \cos(\theta)^2 = 1, $$ as desired.

Addendum: As pointed out by fleablood in the comments, there is a slight hole in the argument: the definition of sine and cosine given above presupposes that the ratios don't depend on the actual triangle. That is, if $\triangle ABC$ and $\triangle A'B'C'$ are right triangles such that $A$ and $A'$ have the same measure, then $$ \frac{a}{c} = \frac{a'}{c'}. $$ This follows immediately from properties of similar triangles, but probably requires some mention in the general development of the theory. Of course, once you make this observation, we could just assume that $c=1$. The Pythagorean theorem implies that $a^2 + b^2 = 1$, and so $$ \sin(\theta)^2 + \cos(\theta)^2 = \left(\frac{a}{1}\right)^2 + \left( \frac{b}{1} \right)^2 = a^2 + b^2 = 1. $$ This argument is basically identical to the one given above, but the computations are slightly more straight-forward.

---

[1] Note that the assumption that $0 < \theta < 90^{\circ}$ is important here, as we have not defined the sine and cosine functions for other values of $\theta$. This is part of why we eventually define these functions using more sophisticated tools in more advanced settings.

[2] I am going to assume that the Pythagorean theorem has already been established, since the argument in the original question seems to assume this result. If one needs a proof, there are one or two on Cut the Knot.

Answer 4

Well, the fundamental theorem of trigonometry is an extra useful identity for us, we all know that it's important.

Here's an approach:

It's basic that: $$0=0$$ Wich is the same if we wrote: \begin{align} 0&=0.t\\ &=0.x\bigg\vert_0^t\\ &=0\times\int_0^t\mathrm{d}x\\ &=\int_0^t2\cos(x)\sin(x)-2\cos(x)\sin(x)\mathrm{d}x\\ &=\underbrace{\int_0^t 2\cos(x)\sin(x)\mathrm{d}x}_{I}-\underbrace{\int_0^t2\cos(x)\sin(x)\mathrm{d}x}_{J}\\ \end{align} Now using some substituions in the integral $I$: $$u=\sin(x)\ \ \ \ \ \ \ \ \ \mathrm{d}u=\cos(x)$$ We'll have: $$I=2\int_0^{\sin(t)}u\ \mathrm{d}u$$ For the integral $J$: $$v=\cos(x)\ \ \ \ \ \ \ \ \ \ \ \mathrm{d}v=-\sin(x)$$ So: $$J=2\int_1^{\cos(t)}v\ \mathrm{d}v$$ Note that the minus sign will dissapear due to the substitution: \begin{align} 0&=2\int_0^{\sin(t)}u\ \mathrm{d}u+2\int_1^{\cos(t)}v\ \mathrm{d}v\\ &=u^2\bigg\vert_0^{\sin(t)}+v^2\bigg\vert_1^{\cos(t)}\\ \sin^2(t)+\cos^2(t)-1&=0\end{align} And here's our identity: $${\cos^2(\varphi)+\sin^2(\varphi)=1}$$ I Hope that you've liked it!

Answer 5

There are many proofs of this identity. We can utilize another trigonometric identity. $$\cos^2(\theta)+\sin^2(\theta)=1\implies\sqrt{\cos(\theta)\cos(\theta)+\sin(\theta)\sin(\theta)}=1$$ Recognize the trigonometric identity under the radicand. $$\sqrt{\cos(\theta)\cos(\theta)+\sin(\theta)\sin(\theta)}=\sqrt{\cos(\theta-\theta)}=\sqrt{\cos(0)}=\sqrt{1}=1$$ Thus, the identity is true for any $\theta\in\mathbb{R}$.

EDIT: Let us begin by recognizing that $\cos^2(\theta)+\sin^2(\theta)$ may or may not be equal to $1$ for any real number $\theta$. Let us prove that it is indeed equal to $1$. \begin{align} \cos^2(\theta)+\sin^2(\theta)&=\cos^2(\theta)+\sin^2(\theta)\\ \cos^2(\theta)+\sin^2(\theta)&=\cos(\theta)\cos(\theta)+\sin(\theta)\sin(\theta) \end{align} If we are permitted to utilize other trigonometric identities, which is not explicitly prohibited in the question, we can quickly finish the proof. \begin{align} \cos^2(\theta)+\sin^2(\theta)&=\cos(\theta-\theta)\\ &=\cos(0)\\ &=1 \end{align} Thus, the identity $\cos^2(\theta)+\sin^2(\theta)=1$ is true for any $\theta\in\mathbb{R}$.

Answer 6

This is the right idea. But I'm confused as to what you are allowed to assume is true by definition or axiom and what you can prove. How are $\cos,\sin$ defined? Do you know the distance formula?

Why are you being asked to prove it? Could it not be assume to be true by axiom and definition?

......

The way I always viewed it, which may or may not be in synch with how you learned it and in which order, was:

First we have the Pythagorean Theorem. I won't bother proving it but... we can google and find many proofs.

The we have converting euclidean geometry to the cartesian plane and find how equations of points as ordered pairs dovetails in with algebraic eqations. I won't go into details but it's basically given Euclid's 5th posulate about parallel lines the horizontal and vertical grids of the cartesian plane are parallel and parellel lines will have equal slopes.

Then we have the distance formula: Two points are $(x_1, y_1)$ and $(x_2, y_2)$ if we create a third point $(x_2, y_1)$ then the line $(x_1, y_1)$ to $(x_2, y_1)$ is a horizontal line $x_2 - x_1$ long and the line $(x_2,y_1)$ to $(x_2, y_2)$ is a vertical line $y_2 - y_1$ long. These two lines form the legs of a right triangle. The line $(x_1, y_1)$ to $(x_2, y_2)$ is the hypotenuse of this line. So by the pythagorean theorem the distance between $(x_1, y_1)$ and $(x_2, y_2)$ is the length of the hypotenuse which is the square root of the sum of the squares of the other legs. So the distance $||(x_1, y_1), (x_2,y_2)|| =\sqrt {(x_2-x_1)^2 + (y_2 - y_1)^2}$.

And then you we have the equation for a circle: A circle is defined as all the points that are equidistance from the center. So if a circle is centered at $(a,b)$ and has radius $r$ the the circle is all the points $(x,y)$ where $||(x,y),(a,b)|| = r$ or in other words so that $(x-a)^2 + (y-b)^2 = r^2$.

So if we have a unit circle centered and $(0,0)$ then the circle is described by all the $(x,y)$ so that $x^2 + y^2 =1$.

And then we define $\sin \theta, \cos \theta$. If $\theta$ is an angle and we look at the point $(x,y)$ on a unit circle centered that cooresponds with the angle, the we define $\cos \theta$ as the $x$ value and $\sin \theta$ as the $y$ value.

Which means as $x^2 + y^2 = 1$ then $\cos^2 \theta +\sin^2 \theta = 1$. There's nothing to prove as that was a well known fact about circles.

.....

Or if you defined $\sin \theta, \cos \theta$ and proportions of right triangle. then

$\cos \theta = \frac {adj}{hypotenuse}$ and $\sin \theta = \frac {opp}{hypotenuse}$ and as $hypotenuse^2 = adj^2 + opp^2$ then $\cos^2 \theta + \sin^2 \theta=(\frac {adj}{hyp})^2 + (\frac {opp}{hyp})^2 = (\frac {hyp}{hyp})^2 = 1$.

....

Okay... I apologize for my initial tone.

If that was your definition of $\sin, \cos$ (and that is a very common way of defining $\sin, \cos$ (although I prefer to use the unit circle definition) then I guess $\cos^2 + \sin^2 = 1$ ISN'T a given after all. (Unless your definition was defined for right triangle with hypotenuse equal to $1$ in which case it is. But still, using the Pythagorean Theorem there isn't much to prove.... merely that dividing by the hypotenuse will scale down to $1$.)

So I guess it shouldn't have surprised me to see you trying to prove it as much as it did.

I apologize. Your proof, for the triangle definition of trig, is correct.

Answer 7

I can solve this using Euler's formula

$e^{i\theta}=\cos(\theta)+i\sin(\theta)$ and $e^{-i\theta}=\cos(\theta)-i\sin(\theta)$.$$\cos^2(\theta)+\sin^2(\theta)=1$$

$$\cos^2(\theta)-i^2\sin^2(\theta)=1$$

$$(\cos(\theta)+i\sin(\theta))(\cos(\theta)-i\sin(\theta))=1\iff (e^{i\theta})(e^{-i\theta}) = 1$$

$$e^0 = 1 \iff 1 = 1$$

$\therefore\theta$ true for any $\mathbb{R}$.

Answer 8

since:

$(cos + sin)^2 = cos^2 + sin^2 + 2*cos*sin$

then:

$cos^2 + sin^2 = (cos + sin)^2 - 2*cos*sin$ ...............(eq #1)

Consider the diagram at

https://www.fullpotentialtutor.com/wp-content/uploads/2022/11/Pythagorean-Theorem-Proof.png.webp

(sorry, I am new and not allowed to post images yet)

if we consider area then $(a + b)^2 = c^2 + 4 * \frac{(b * a)}{2}$

Rearranging:

$(a + b)^2 - 2 * (b * a)= c^2$

or:

$\frac{(a + b)^2}{c^2} - 2 * \frac{b * a}{c^2} = 1$

or:

$(\frac{a}{c} + \frac{b}{c})^2 - 2 * \frac{b}{c} * \frac{a}{c} = 1$

we can substitute $cos = \frac{b}{c}$

and $sin = \frac{a}{c}$

and we get:

$(sin + cos)^2 - 2*cos*sin = 1$

Substituting eq #1:

$sin^2 + cos^2 = 1$

Answer 9

I have thought of a simpler approach

I am new to this site and am not yet allowed to post images, so please consider the triangle at:

Wiki Triangle

We know that $\angle ABD = \angle ADC$ and shall focus on those two angles

$\cos = \frac{BD}{BA} = \frac{AD}{AC}$

$\sin = \frac{AD}{BA} = \frac{DC}{AC}$

So substituting into $\cos^2 + \sin^2 = 1$

$\frac{BD * AD}{BA * AC} + \frac{AD * DC}{BA *AC} = 1$

As $BD + DC = BDC$

$\frac{(BDC - DC) * AD}{BA * AC} + \frac{AD * DC}{BA *AC} = 1$

$\frac{BDC*AD}{BA*AC} - \frac{DC* AD}{BA * AC} + \frac{AD * DC}{BA *AC} = 1$

$\frac{BDC*AD}{BA*AC} = 1$

Since, $\cos = \frac{AD}{AC}$ and

$\frac{BDC}{BA} = \frac{1}{\cos}$ then

$\frac{\cos}{\cos} = 1$