I have a degree in mathematics, but let's digress for a moment. I promise to talk about math a little bit later.
I read your question.
I think that your question is very strange.
Let me ask you a question of my own:
“When you last visited planet Mars, did you enjoy the Unicorn reserve significantly more than the Manticore pavilion?”
Notice that I have assumed that planet Mars has a Unicorn zoo.
Also, have assumed that you have personally set foot on planet Mars sometime in your past.
In your own question, you have repeatedly assumed things which are not true.
At the risk of creating a straw-man, you seem to think that for any word in the English language there exists a "correct" definition for that word.
Consider the following words:
- valid
- statement
- formula
- sound
- argument
Words are like screwdrivers. If you are trying to put in a Phillips head screw, then it is in your own best interest to use a Phillips head screw-driver, instead of a hammer, or something like that.

Well, the laws of physics do not stipulate what a “statement” is.
The fabric of the universe does not care what a “statement” is.
There is no correct definition for what a “statement” is.
Use whatever definition of "statement", you find most useful to convey your ideas to other people.
At one point, you asked the following:
Does mathematical logic have a concept for "statement"? Does "statement" correspond to “formula” in mathematical logic?
Mathematicians use statements all of the time. If you were to read a typical mathematical proof, you would find a proof is less than 25% quadratic equations, or stuff like $\sqrt{37} = \sqrt{\frac{73^2-1}{12^2}}$.
The following is an example of a mathematical statement:
Consider a diagram drawn by putting dots on a sheet of paper. Now draw some lines connecting at least a few of those dots.
Suppose that there is at most one line connecting the same pair of dots.
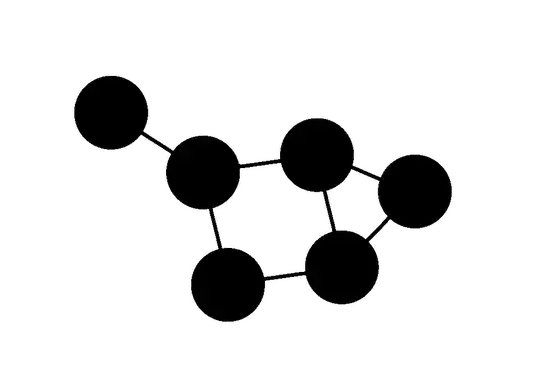
if every one of your dots has at least 3 lines coming out of it, then there is at least one loop-de-loop (cycle) in your drawing containing an even number of edges. That is, if at least 3 lines emanate from each dot, then there will be at least one loop in the drawing having 2, 4, 6, 8 edges, etc. .
Actually, I am not being entirely honest. A mathematician would probably write:
For any graph G, if every vertex in G has degree at least 3, then G contains at least one cycle containing an even number of edges.
Most mathematical proofs have more English-like statements, than they have formulas.
Does mathematical logic have concepts for "validity" and "soundness" of "arguments"?
Sure.
The following is an example of a valid, but un-sound, mathematical argument:
- Every real number is an element of $\{4*n: n \in \mathbb{N}\}$ (PREMISE)
- All elements of $\{4*n: n \in \mathbb{N}\}$ are even (PREMISE)
- Every real number is even (from lines 1 and 2).
When I wrote that "every real number is an element of $\{4*n: n \in \mathbb{N}\}$" I meant that "every real number is a whole number divisible by 4, such as 8, or 404$"
You also asked,
Does mathematical logic have a concept for "argument"? Does "argument" correspond to a one-step derivation (derivation by applying just one inference rule) in mathematical logic?
What philosophers call an "argument" mathematicians call a "proof".
Does "argument" correspond to a one-step derivation.
The short answer is:
- No, arguments are not one-step derivations.
The long answer is:
- It would be highly unusual to define an “argument” to be a one-step derivation, but it is allowed. I have degree in mathematics, but I have never read a book, or journal article, where a mathematician defined “argument” to mean something with only one-step. However, you are allowed to define “argument” as a one-step derivation.
Words are tools.
If you find a Phillips head screw-driver to be more useful than a wood saw, then use the Phillips head screw-driver.
Not all mathematicians use their vocabulary the same way that Ebbinghaus does.
Competent mathematicians will define their nomenclature in the paper or book they publish.
That way, if you do not already have to know what a “formula” is or an “interpretation,” you can read the definition given in the paper.
You wrote,
Ebbinghaus' Mathematical Logic says "a formula is valid if and only if it holds under all interpretations". How is that related to "validity" of "argument"?
In the context of classical Greek logic and philosophy, the following is an example of an “argument”
- If I bought a lottery ticket last Sunday, then I would have won the lottery (premise)
- Not(I would have won the lottery) . . . . . . . . . . (Premise)
- NOT( I bought a lottery ticket last Sunday . . . . . . from lines 1, 2 Modus Tollens
Let us explain what a formula is.
We can also explain what an interpretation is, etc. .
I will endeavor to clarify what all of those things are in way which is consistent with the lottery tickets and Modus Tollens stuff beings an example of an “argument”.
In Ebbinghaus' book a formula has variables in it.
$\text{if} P \text{then} Q$ is an example of a formula.
Maybe, $X + Y \leq Z$ is a second example of a formula.
An interpretation of a formula is formed by replacing variables in the formula by non-variables.
For example, 4 + 2 would an interpretation of the formula X + Y
if I hated my pet dog then I ated my pet dog is an interpretation of the formula if P then Q
Ebbinghaus' says that,
"a formula is valid if and only if it holds under all interpretations"
Well, suppose that (X + Y) < (X + 2*Y) a formula
Also, suppose that the set of interpretations of $(X + Y) < (X + 2*Y)$ is the set of all statements formed by replacing $X, Y,$ and $Z$ with any positive whole numbers.
Then, (7 + 1) < (7 + 2*1) is an example of an interpretation of the formula (X + Y) < (X + 2*Y)
Then, $(X + Y) < (X + 2*Y)$ is a VALID formula.
No matter how we interpret the formula, the resulting statement is a true statement.
No matter what specific numbers are chosen for $X$ and $Y$, we have $(X + Y) < (X + 2*Y)$
The following is a formula:
1. If P then Q
2. Not Q
3. P . . . . from lines 1, 2 Modus Tollens
If you replace all of the variables (such as P) by something like I ated my pet dog then the resulting text is an interpretation of the original formula.
If every interpretation of a formula “holds” (is correct in some way, shape, or form) then we say that the formula is valid.
True versus Valid
There is a reason that people mix-and-match words like true and valid
Suppose you have the outline of a philosophical argument. Maybe instead of outline you call it a schema or an argument-form. An outline looks just like an argument except that it contains place-holder variables, such as “$P$” and “$Q$” instead of “it is raining outside.”
For any outline of an argument there exists a statement which is true if the argument-outline is valid. Also, this statement is false if the argument-outline is invalid.
1. if P then Q . . . . . . . . . premise
2. not Q . . . . . . . . . premise
3. not P . . . . . . . . conclusion
The argument-thingy above is valid if and only if the following statement is true:
$\forall P, Q \in \{0, 1\}, 1 = [(if P then Q) and (not Q)] then (not P)$
Converting arguments into statements is easy:
- Construct one big premise by conjoining all small premises together using the
AND operator.
- Replace “$A$” in the statement “$\forall P, Q \in \{0, 1\}, 1 = A \implies B$” with the gaint merged premise completed in step 1.
- Replace “$B$” in the statement from step 2 with the conclusion of the original argument.
There difference between the words true and valid is not as significant as you think.
An argument is a statement and the statement is true if the argument is valid.
Sweeping the Universal Quantifier Under the Rug
Most of the reason some logicians talk about formulas and interpretations is to avoid using the symbols $\forall$ and $\exists$.
Most logicians will tell you that the sentential calculus or “zeroth-order logic” or “propositional logic” does not use the quantifiers $\forall$ or $\exists$.
Use of $\forall$ and $\exists$ is strictly forbidden!... or so they say.
Those logicians are lying to themselves.
Note that an argument-form in propositional logic is a valid argument form if and only if $\forall$ statements $P$, $Q$, $R$, etc... if the premises are true, then the conclusion is true.
The reason that Ebbinghaus' talks about ALL interpretations of a formula is so that his formulas do not contains words like “every” or “all” or the symbol $\forall$.
A formula should look like this:
$\forall X \in \{n \in \mathbb{N}: n > 999\}, X > 0$
However, Ebbinghaus is terrified of using the universal quantifier.
He is also avoiding set theory.
Therefore, Ebbinghaus’ formula looks like:
$X > 0$
There is no universal quantifier here! Nope!
Ebbinghaus then says that an “interpretation” of the formula is created by replacing $X$ with any whole number strictly greater than $999$.
$X > 0$ is a valid formula if any only if the $\mathcal{SET}$ of $\mathcal{ALL}$ interpretations are true.
$5005 > 0$ is an example of an interpretation of $X > 0$.
Just replace the $X$ with any allowed number.
There are a non-finite number ofy interpretations of $X > 0$, but each interpretation is true if variables are whole numbers strictly greater than $999$
One Last Observation
Note that:
people often use the word “argument” to mean “a verbal confrontation between two parties. Usually, both parties are people, and people experience angry emotions while arguing with each other.”
In other contexts “argument” means “input parameter.” For example, “$x$ is an argument to the function described by the formula $f(x) = x^{2} + 55$”
Notice that the passage “the formula $f(x) = x^{2} + 55$” might even use the word “formula” differently than how I explained the word “formula” earlier.
People sometimes use the word “string” to refer to cotton twine used to tie items to the roof of a car. Other times, particularly in computer science, a “string” is a passage of text, such as your phone number, or the password to your email. The entire contents of a famous book, such as a war and peace, is also a string.
If anyone tells you that one way to use a word is correct, and all other ways to use that word are incorrect, then that person is not telling the truth.
Words are man-made tools. Please feel free to use them as you see fit.
You seem to think that there is some concrete way mathematicians use words like, “literal”, “variable”, “formula”, “valid,” etc... There is not really any standard nomenclature in mathematical logic.
I encourage you to stop seeking out the true meaning of the word “valid” and instead you start choosing how to define “valid” so that your definition is useful to other people.
It is not written on planet Saturn whether or not a tent is a house or not.
If you peer at an atom with an electron microscope, it will not say “every fruit-smoothie is not a complete lunch”
In the past, someone defined what the words “tent” and “house” meant.
Someone also invented phrases like, “complete meal” and “fruit smoothie”
The question “Is a tent a house?” presumes that that the question “What is a house?” has a definitive correct answer.
Words are like hammers, screw-drivers, saws, pliers, wrenches, etc...
I don’t think it is written into the fabric of the universe what these words mean.
Words are tools.
Mathematicians invent words; they define them on-the-fly.
If a mathematician thinks it is useful to define a “cactus”, then the mathematician will usually do so.