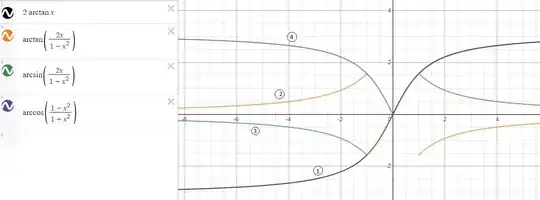
I have these three equations: $$2\arctan(x) = \arcsin(\frac{2x}{1+x^2}),\left |x\right|\leq1$$ $$2\arctan(x) = \arccos(\frac{1-x^2}{1+x^2}),x\geq0$$ $$2\arctan(x) = \arctan(\frac{2x}{1-x^2}),\left |x\right|<1 $$ I can verify these by simple substitution taking $x = \tan\theta$ for some $\theta$ but I could not understand why these conditions for $x$ are given. I can see their graphs makes sense but is there an algebraic way of proving/verifying these conditions?
Also the graph is:
An exercise I found helpful.
Consider the intersection of the line $y = tx$ and the circle $x^2 + y^2 = 2x$
The circle has radius 1 and is centered at $(1,0)$
$x^2 + (tx)^2 = 2x\\ x = \frac {2}{1+t^2}\\ y = \frac {2t}{1+t^2}$
Now lets translate everything one unit to the left. Yes, we could have calculated the intersection of $x^2+ y^2 = 1$ and the line $y = t(x+1)$ but the algebra is simpler this way.
$x = \frac {2}{1+t^2}-1\\ x = \frac {1-t^2}{1+t^2}\\ y = \frac {2t}{1+t^2}$
Do these equations look familiar? What are $x,y,t$ geometrically / trigonometrically?
The line and the circle and the x axis form an angle on the circle, which has half the measure of the central angle to that same arc.
$t = \tan \frac 12 \theta$
And of course,
$x = \cos \theta\\
y = \sin \theta$
Regarding the domain restrictions. If $t> 1$ the line $y = t(x+1)$ will be intersecting the circle in QII.
$\arcsin (\frac {2t}{1+t^2})$ will return a value corresponding to a point in QI
Similarly if $t < 0$
$\arccos (\frac {1-t^2}{1+t^2})$ will return a value for a point in QI or QII while our reference point is actually in QIII or QIV
I found this exercise to more helpful to build intuition than mechanically chug through the trig identities.
Here would be the mechanical approach:
$\sin (\arctan \frac {a}{b}) = \frac {a}{\sqrt {a^2 + b^2}}\\ \cos (\arctan \frac {a}{b}) = \frac {b}{\sqrt {a^2 + b^2}}\\ \theta = 2\arctan t\\ \sin \theta = 2\sin(\arctan t)\cos(\arctan t) = 2\frac {1}{\sqrt {1+t^2}}\frac {t}{\sqrt {1+t^2}} = \frac {2t}{1+t^2}\\ \cos \theta = \cos^2(\arctan t)-\sin^2(\arctan t) = \frac {t^2}{1+t^2} - \frac {1}{1+t^2}= \frac {1-t^2}{1+t^2}$
Hint: Further to my comment,
Let $\arctan x=\theta\implies \tan \theta=x$, where $ \theta \in (-\pi/2,\pi/2)$ Why? Because $\tan$ is invertible there. Isn't it?
$\sin 2\theta=\frac{2\tan\theta}{1+\tan^2\theta}=\frac{2x}{1+x^2}\tag{1}$
Note that $2\theta\in (-\pi,\pi)\implies$ we can't take inverse of $\sin $.
In order to take inverse of $\sin$, we should have $2\theta \in [-\pi/2,\pi/2]$, which is clearly true if $-\pi/4\le \theta\le \pi/4$ so that $x=\tan \theta \in [-1,1]$
Hence, if $2\theta\in [-\pi/2,\pi/2] $, then we can take inverse in $(1)$ to get:
$2\theta=\arcsin \frac{2x}{1+x^2}\implies 2\arctan x=\arcsin\frac{2x}{1+x^2}$, where $2\theta\in [-\pi/2,\pi/2]\implies |x|\le 1 $
Similarly, prove the rest of the two.
Response to comment: Definition of $\arcsin, \arctan$:
I have used principal values of arc sin, arc tan. That is to say, $\arcsin x=\phi$ if $x=\sin\phi$, where $\phi\in [-\pi/2,\pi/2]$
For tan, $\arctan y=\psi$ if $\tan\psi =y$, where $\psi\in [-\pi/2,\pi/2]$.
The last equation says (by the definition of arctan) that if $\tan\theta=x$, then $\tan2\theta = \frac{2x}{1-x^2}$; so this is just the double-angle formula for tan.
The first two equations can be derived from the last equation by drawing a right triangle with sides $2x$ (opposite) and $1-x^2$ (adjacent) and hypotenuse $1+x^2$, and thereby noting that the angle whose tangent is $\frac{2x}{1-x^2}$ is the same as the angle whose sine is $\frac{2x}{1+x^2}$, which is the same as the angle whose cosine is $\frac{1-x^2}{1+x^2}$.
