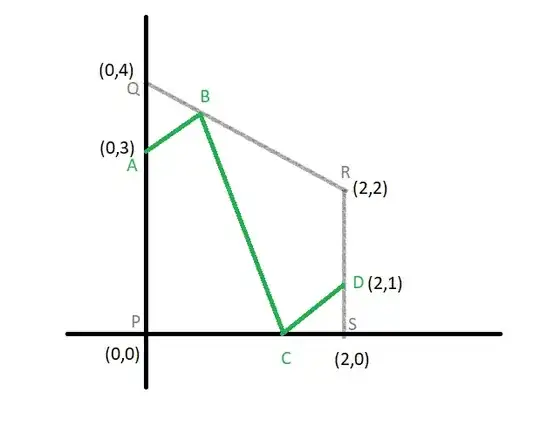
I tried using coordinate geometry to find the distance AB,BC and CD and then finding their minimum by partially differentiating the equations. This yielded a rather complicated equation which I could not solve.
I'm sure there must be a more direct and simpler approach to this question, but I am simply hitting dead ends.
Any hints on how to solve the question?
Thanks a lot in advance!
Regards