Do I understand the difference between $\implies$ and $\to$?

Question

I am taking a course in Discrete Mathematics. In the course we are using $\to$ for implication and have been discussing truth tables and the like. But something was said about this being the same as $\implies$. It seemed strange to me that if they are the same, why not just use one of the symbols. I dug around and find that there is a difference.

I know that in the day to day life of a mathematician, whatever difference there is, it isn't really much to worry about. But there is supposedly a difference. I know that there are a number of other questions/answers on this site that discuss this, but I am still a bit confused. Here is my current understanding. Please tell me if I am thinking about it the right way

First my understanding:

---

A proposition is the same as a statement.

When $A$ and $B$ are propositions, then $A \to B$ is the proposition with the truth table that is only false when $p$ is true and $q$ is false.

When proving a theorem something is assumed to be true. From this one makes arguments that lead to the conclusios. We then use $A \implies B$ to say that since we know $A$ is indeed true, then $B$ must also be true. To $\implies$ is not a strict logical symbol with a truth table. We only use this to say that something is true because of something else.

If I know that $x$ is equal to $1$ and I want to say that from this follows that $x^2 = 1$, then I would use $\implies$. So I may say "We know that $x=1 \implies x^2 = 1$".

So far so good.

Let's say I want to define a set. If I consider the two sets $$ A = \{x\in \mathbb{R}: x^2 =1 \to x\geq 0\} \\ B = \{x\in \mathbb{R}: x^2 =1 \implies x\geq 0\} $$

Here then $A = \mathbb{R}\setminus \{-1\}$ because for these numbers the proposition/statement $(x^2 =1 \to x\geq 0)$ is true.

And $\implies$ in $B$ doesn't make sense because I am not asserting anything. This would be the same reason that if I make the theorem that: for all real numbers $x$, $x^2 = 1 \implies x = 1$, then this is an incorrect theorem.

If I make the definition saying that a real number $x$ is foo if $x^2 = 1 \implies x =1$, then the only number that is foo is $1$.

Is all this correct?

---

I understand that mathematicians use $\implies$ when maybe they "should" use $\to$ and this doesn't bother me. I am just trying to understand.

(You should have a "did-I-understand-this-correctly tag.)

Answer 1

I'm not sure about other fields, but in logic, '$\implies$' is used to denote logical implication in two senses:

1. The validity of $\phi\rightarrow\psi$; and
2. An implication outside the context of a structure (i.e. a "meta-theoretic" or "real world" implication).

To explain (1), Usually '$\rightarrow$' is a defined symbol corresponding to a certain truth table. As a result, "$\phi\rightarrow\psi$" is only defined when we know the truth values of $\phi$ and $\psi$. "$\phi\implies\psi$" is a stronger statement saying that no matter the context in which we consider $\phi$ and $\psi$, $\phi\rightarrow\psi$ is true. To say the same things in model-theoretic terms, $\models$ "$\phi\rightarrow\psi$" is the same as $\phi\implies\psi$. For example, in the context of $\mathbb{R}$, "$x^4=1\rightarrow x\in\{-1,1\}$" is true. But in the context of $\mathbb{C}$, "$x^4=1\rightarrow x\in\{-1,1\}$" is false. So we shouldn't write '$\implies$' in place of '$\rightarrow$' (at least with this interpretation, since obviously many mathematicians have their own preferences). To introduce some notation you may be unfamiliar with, "true in the context of ..." is basically just written with $\models$. So above, we would say $$\mathbb{R}\models\forall x\ (x^4=1\rightarrow x=-1\text{ or }x=1)$$ but $$\mathbb{C}\models\neg\forall x\ (x^4=1\rightarrow x=-1\text{ or }x=1)$$

To explain (2), again, '$\rightarrow$' is taken to be part of a formal language. We build up the notion of truth in a structure using this language. We sometimes use '$\implies$' to denote implication outside of this formal language. More succinctly, '$\rightarrow$' appears in formulas whereas '$\implies$' appears outside of them. So something like "$A\models \phi\implies B\models \psi$" makes sense but "$A\models\phi\rightarrow B\models\psi$" doesn't (in general).

These two uses aren't completely incompatible: $\phi\implies\psi$ is equivalent to the statement that for all models $M$, $M\models\phi\implies M\models\psi$. An easy example of this is things like $(\phi\text{ and }\psi)\implies \phi$, or more complicated things involving quantifiers: $\exists x\ \forall y\ \phi(x,y)\implies \forall y\ \exists x\ \phi(x,y)$.

Answer 2

In mathematical logic (and I'm way outside my domain of expertise) there are two separate things you can say about $p$ and $q$. One is $p \to q$, which you explained nicely in terms of truth tables.

The other is $p \implies q$. That's used (at least in some places, like the Isabelle/HOL proof assistant) to mean that using the rules for fiddling with formulas (the "deduction rules" of your logic) you can transform $p$ to $q$. People say things like "$q$ can be deduced from $p$".

If your logic (set of deduction rules) is nice (and I forget the right word for this), everything that can be deduced from known-to-be-true statements should also be true. If your logic were really nice, then every true statement could be deduced to be true from basic known-to-be-true statements.

You might be asked "what do you mean by 'a logic'? Isn't there just one logic, like, what Aristotle did?" The answer is no, there are many (predicate logic, first order logic, higher order logic, ...) and each has its own place.

But as you may have inferred from your teacher's remarks, most practicing mathematicians who are not logicians...spend almost no time thinking about this. Lots of them (like me, a year or so ago) can't really even make clear the distinction. (And I've been doing mathematics for about 50 years!)

@MauroAllegranza can make what I've said above FAR more clear, and can correct any of my infelicitous glitches.

Answer 3

Complementing the other answers, I'd say:

tl;dr: $\rightarrow$ and $\Rightarrow$ are implications from different meta levels.

Personally, I learned (and I still am!) distinguishing meta levels the most when formalizing mathematics with the computer and proof assistants. Namely, there you are a) forced to formalize some meta levels on your own and b) you usually get some type checking errors when mixing up different meta levels.

Hence, I'd like to sketch four meta levels pertaining proof assistants, and on every level identify a form of implication. At first sight, this might seem as an extreme overkill for a student of your level, but perhaps you can still take home some (perhaps philoshopic?) messages even if you don't understand everything at once.

A proof assistant and a formalization therein may feature the levels below. Throughout the answer, I tried using standard terminology with the exception of the numbering of the levels. That has been totally made-up by me for the sake of this answer.

1. A system (Coq, Isabelle, MMT, ...)

   In the core of most proof assistants, judgements are used in the underlying implementation (in a programming language), to represent and compute that something that the user has entered is valid. For instance, you might imagine an "is-valid judgement". To infer such judgements, the system might use inference rules. You might think of them as functions in a programming language getting judgements as input and yielding judgements as output. Often, such rules can be pretty expressive; on pen-and-paper they are often denoted in the following form:

   

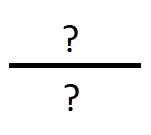
   You can read this as: "if we inferred the thing above the line, then we can also infer the thing below the line." I will show a concrete rule in the next paragraph, but for now, it suffices to see this as a first form of implication.

   In the following, I will draw further examples from the proof assistant Coq to substantiate my points, but rest assured that the concepts are sound and useful in general, too.

2. A mathematical foundation (usually some flavor of type theory or set theory)

   To actually be able to do and write down anything, you need a foundation — without them there is simply nothing to draw from. In mathematics, foundations are often left implicit by working mathematicians (outside of logic that is), however, most would probably say that they work in ZF set theory. Likewise, a proof assistant also needs a foundation.

   Foundations for proof assistants can often be conveniently stated with the rules discussed before. For instance, Coq uses the so-called calculus of constructions as its foundation. Here is an arbitrary rule from its documentation:

   

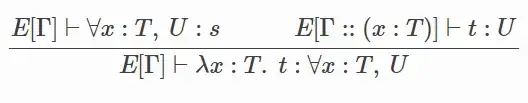
   Don't worry — you don't have to understand or even parse all symbols. Let me just tell you that this rule (partly) implements functions. In other words, we need this rule among others so that end users using Coq can write functions (as in from programming languages) therein. And, you may believe me on that, functions correspond to yet another form of implication, although this time at the foundational level.

3. A logic (first-order logic, higher-order logic, modal logic, ...)

   Now given a system and its foundation, we of course want to express theorems and proofs in a proof assistant. For that, we need a logic to work with. Note that the line between systems, foundations, and logics might be blurry depending on the system in use. Some systems hardcode foundations and logics whereas others such as MMT have foundation-independence as one of their main goals. With Coq, the shipped standard library comes equipped with some logic. For didactic reasons, let us simulate (re)implementing a logic in Coq and for simplicity, let us restrict to propositional logic (PL). Of course, PL is far too weak for anything useful. Nevertheless, in Coq this could look as follows:

   Inductive PL :=
     | impl: PL -> PL -> PL
     | and:  PL -> PL -> PL
     | or:   PL -> PL -> PL
     | neg:  PL -> PL.
   

   Again, you don't need to understand the semantics of this in detail. It just says that we define a type called PL and for writing down things of PL we got 4 postulated constructors. For instance, if x is of PL, then we can write down impl x x (to represent $x \rightarrow x$). Concretely, per the code above, the constructor named impl takes two subformulae from PL itself and returns a new formula — again from PL (... -> PL). The same holds true for and and or. Last but not least, neg is a constructor taking only one formula as input and, as before, outputting a new formula.

   Remember when you were taught propositional logic and were told that exactly those connectives exist, how many arguments they have, and how they can be combined? This is exactly it, just formalized in Coq.

   The implication on this meta level is impl. This variant of implication might be the closest to what you would have understood as "implication" so far in your education. (This is not intended to sound condescending.)

4. A theory within the logic (e.g., a logic within a logic)

   Let's assume we work a bit harder on the logic meta level and instead of propositional logic we formalize the more elaborate case of first-order logic (FOL). Then, within FOL we are free to formalize further things, e.g., PL itself. Note that by "PL" I mean the (philosophic?) concept of propositional logic and not the instantiation from the last point, which I typeset as PL. Concretely, PL can be seen as the FOL theory containing

   • four function symbols: impl', and', or' with arity 2, and neg' with arity 1,
   • and various axioms, e.g., ∀xyz. ¬(impl' x y = and' x y) (for those who understand: effectively demanding the function symbols to be constructors of an inductive data type).

   Here evidently, impl' is (supposed to be) yet another form of implication — building upon the previous meta level from 3.

Let me come full circle with your question. First, you might imagine the implication from level 3 as $\Rightarrow$ and the one from level 4 as $\rightarrow$. Second, you asked which of the following notations is correct:

$$A = \{x\in \mathbb{R}\mid x^2 = 1 \rightarrow x\geq 0\}\\B = \{x\in \mathbb{R}\mid x^2 =1 \Rightarrow x\geq 0\}$$

This depends on which level you formalize what $\{\ldots\}$ is. If you formalize it on level numbered 3 above as something of the form $\{x \in \_ \mid x \Rightarrow y\}$ where $x$, $y$ themselves stem from level 3, too, then only variant $B$ is correct. But note that this implies that the expressions $x^2 = 1$ and $x \geq 0$ are from level 3 (PL), too!

If on the other hand $\{\ldots\}$ has been defined on the level numbered 4 above, only $A$ is correct. But then again, $x^2 = 1$ and $x \geq 0$ must be expressions of the fourth level (well-formed terms within the given FOL theory there).

As a last note, the requirements of where the subexpressions come from stated in the last two paragraphs are often relativized. For instance, for level-4-expressions $x, y$, it might make sense to speak of $x \Rightarrow y$ to mean "$y$ is derivable from $x$ via some application of level-4-rules". Sometimes, this is implies $x \rightarrow y$. Sometimes not. Hence, be cautious about mixing meta levels, especially when working in logics or formalizing them.