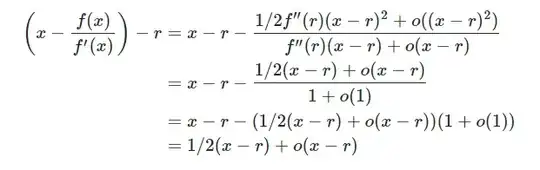In the picture above how does one go from the second equal sign to the third? This is a screenshot taken from the first answer from Newton Raphson Method for double roots. In my mind this just does not seem to be correct, how can one go from dividing by $1+ o(1)$ to multiplying by it?
Yes this works. Here is a "sketchy way" to verify this. Going by the definition the rigorous way presumably also works but might not be as instructive.
Let $f(x)$ be a general function of $x$. Then \begin{align*} \frac{f(x)}{1 + o(1) } &= \frac{f(x) + f(x) o(1) }{1 + o(1) } - \color{red}{\frac{f(x) o(1)}{1 + o(1) }}\\ &\overset{!}= \frac{f(x) + f(x) o(1) }{1 + o(1) } - \color{red}{f(x)o(1)} \\ &= f(x) \cdot \color{blue}{(1 - o(1) )} \\ &\overset{!}= f(x) \cdot \color{blue}{(1 + o(1) )} \end{align*}
The step between the two red terms is key. Since $1 + o(1) \sim 1$ as $x \to \infty$, the two red terms have roughly the same size.
The step between the two blue terms work in this case where we're just discarding the lower order terms. In this situation, $o(1)$ is the same as $-o(1)$. (NOTE: There are other situations where this matters, for example when the $\pm o(1)$ term is in the base of an exponential function.)
Another way to see what is going on is to set $y := o(1)$ and notice
$$ \frac{1}{1 + y} = 1 - y + y^2 - y^3 + \dots $$
So if $y \ll 1$, then $\frac{1}{1 + y} \approx 1 - y$. Again, this is a situation where $-y$ is just as negligible as $+y$, so the last step is to say $1 - y \approx 1 + y$ and we get the desired approximation.
