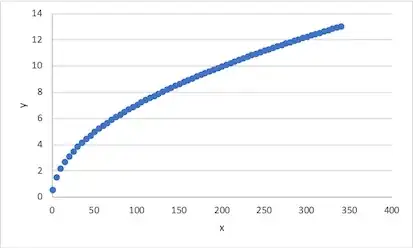
I am interested in knowing the value of the fraction $y = \frac{\Gamma(\frac{x+1}{2})}{\Gamma(\frac{x}{2})}$ for different non-negative values of $x$.
Plotting $y$ suggests that the value of the fraction follows a power function of the form $ax^p$.
Using power regression in Excel, I find $a=0.6445$ and $p=0.5179$. Although, the $R^2$ value of $0.9987$ is quite high, I am wondering:
If it exists, what is the closed-form expression to describe the relationship between $y = \frac{\Gamma(\frac{x+1}{2})}{\Gamma(\frac{x}{2})}$ and $x$?
Although I am primarily interested in the particular fraction presented in this question, more general answers are also welcome.