0

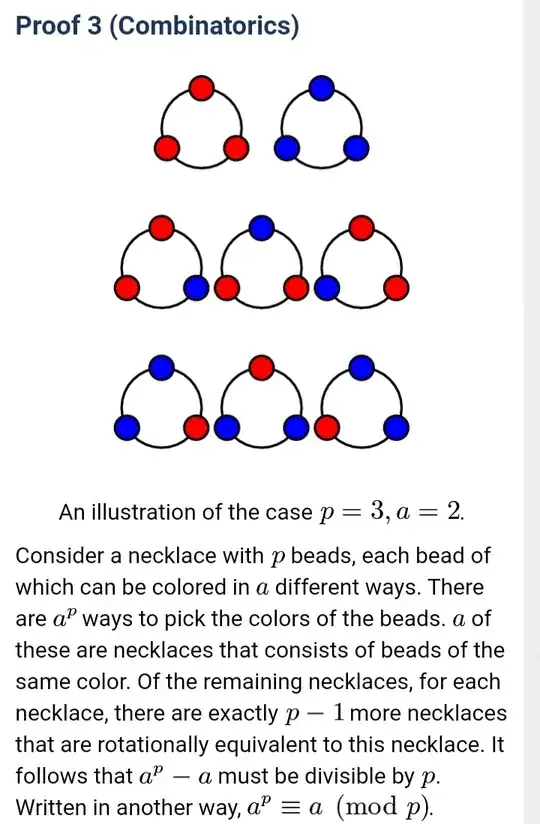
The following image is the necklace proof of Fermat's little theorem taken from https://artofproblemsolving.com/wiki/index.php/Fermat%27s_Little_Theorem#Proof_3_.28Combinatorics.29

My understanding of this proof is is that there is no need for p to be a prime number. And that for all p, where p is any positive integer, the proof given below should hold. Where am I being wrong ?

enter image description here

P.S: Fermat's little theorem states that if p is a prime number, then for any integer a, the number (a^p − a) is an integer multiple of p.

Hemant Agarwal
  • 211

1 Answers1

1

If $p=4$ you can consider the alternating black and white necklace. It only produces two different neclaces when you rotate.

You need $p$ to be prime so that every necklace that isn't all the same color yields $p$ different ones when you consider the $p$ rotations.

Asinomás
  • 105,651
  • How do you know that if and only if p is a prime number then "every necklace that isn't all the same color yields p different ones when you consider the p rotations". – Hemant Agarwal Sep 13 '20 at 06:40
  • 1
    Because the number of different necklaces has to be a divisor of $p$ – Asinomás Sep 13 '20 at 06:42
  • "Because the number of different necklaces has to be a divisor of p." How does this statement prove that p is a prime number ? – Hemant Agarwal Sep 13 '20 at 07:05
  • 1
    Oh, for the other direction of the implication you can take a coloring that repeates every $d$ colors where $d$ is a direction of $p$. – Asinomás Sep 13 '20 at 17:26