Finding the area under the inequality $\sin^2 \pi x + \sin^2 \pi y \le 1$ for $x,y \in [-1,1]$

Question

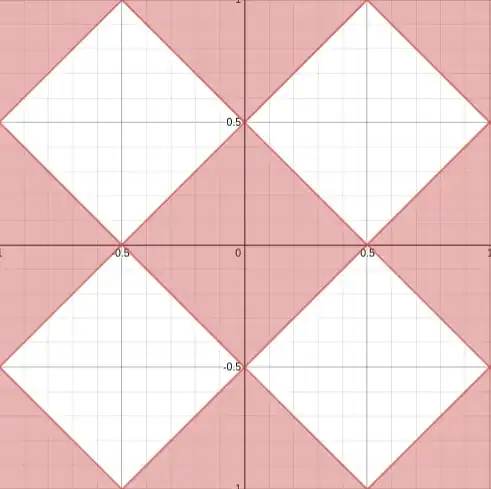
Find the area under the inequality $$\sin^2 \pi x + \sin^2 \pi y \le 1 \text{ for } x,y \in [-1,1]$$

I coudn't do this problem without using a graphing calculator:

It's easy to see now that in each quadrant, the area is $1/2$ unit, so the total area would be $2$ units.

How would one do this without access to a graphing calculator? Looking at the graph, It looks like there is a pattern I am missing out on. One thought would be to make the implicit inequality explicit, and obtain $$|\sin \pi y \le \cos \pi x|$$ but I still couldn't couldn't graph this manually.

Answer 1

We have that

$$\sin^2 \pi x + \sin^2 \pi y = 1 \iff \sin^2 \pi x=\cos^2 \pi y \iff \sin \pi x=\pm\cos \pi y$$

and since by definition

$$ \begin{cases} \sin A= \cos B \iff A=\frac \pi 2\pm B+2k\pi \\\\ \sin A= -\cos B=\cos (-B) \iff A=-\frac \pi 2\pm B+2k\pi \end{cases} $$

we obtain

$$ \begin{cases} \pi x=\frac {3\pi} 2 \pm \pi y \iff x=\frac 32 \pm y\\\\ \pi x=\frac \pi 2 \pm \pi y \iff x=\frac 12 \pm y\\\\ \pi x=\frac \pi 2 \pm \pi y \iff x=\frac 12 \pm y\\\\ \pi x=-\frac {3\pi} 2 \pm \pi y \iff x=-\frac 32 \pm y \end{cases} $$

from here we can obtain the area under the inequality.

Answer 2

Use Prove that $\cos (A + B)\cos (A - B) = {\cos ^2}A - {\sin ^2}B$

$$\sin^2\pi x\le\cos^2\pi y$$

$$\iff\cos\pi(x+y)\cos\pi(x-y)\ge0$$

Case$\#1:$

If $\cos\pi(x+y)\ge0,2n\pi-\dfrac\pi2\le\pi(x+y)\le2n\pi+\dfrac\pi2\iff2n-\dfrac12\le x+y\le2n-\dfrac12$

and then we need $\cos\pi(x-y)\ge0\iff 2m-\dfrac12\le x-y\le2m-\dfrac12$

where $m,n$ are integers

Case$\#2:$

$$\cos\pi(x+y)\le0,\cos\pi(x+y)\le0$$

Answer 3

We can write $$ z(x,y)=\dfrac{\sin^2\pi x}{\cos^2\pi y} \ge 1$$ because $\le1$ is inadmissible. The total area is partitioned into two regions in case of equality by two sets of straight lines having slopes $\pm 1$: $$\pm x\pm y=\pm \dfrac{k}{2}$$

for integer$k$ which makes area vanish by virtue of symmetry wrt either axis.