probability involving two points inside a sphere

Question

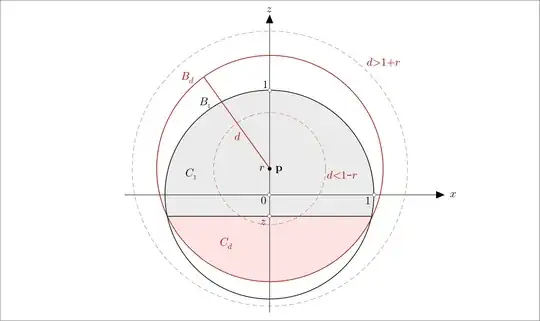
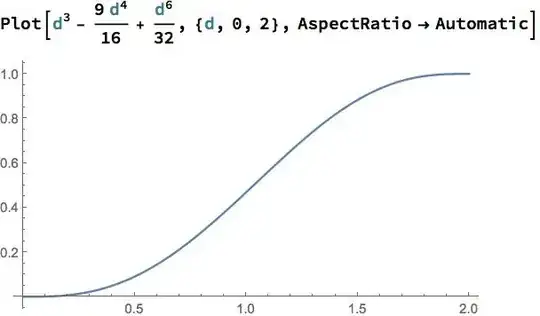
Find the probability that two randomly selected points inside a sphere of radius $r,$ are at most $d$ apart, where $0\leq d \leq 2r$.

I've seen several answers on Math Stack Exchange about this, but I really haven't been able to understand how to come up with the probabilities. For instance, this post has two answers, none of which I can understand. Could someone direct me to some resources to better understand how to derive $3$-dimensional integrals such as the one in the answer? I understand that I can pick the first point and modify the coordinate system so that it has coordinates at $(0,0,z)$ and that makes things easier to visualize and compute. Also, since the probabilities are the same regardless of what $r$ is by symmetry, I can assume WLOG that $r=1.$ But how did @Empy2 derive the integral? The integral from $0$ to $1$ of $z^2$ wrt $z$ in the denominator I presume represents the probability of the sample space?

Answer 1

Two random points ${\bf p}$ and ${\bf q}$ are uniformly and independently distributed in the unit ball $B_1\subset{\mathbb R}^3$, and a distance $d\in[0,2]$ is given. We want to know the probability $F(d)$ that $|{\bf q}-{\bf p}|\leq d$.

Denote by $p_d(r)$ the probability that $|{\bf q}-{\bf p}|\leq d$, conditioned on the assumption ${\bf p}=(0,0,r)$ with $0<r<1$. On account of spherical symmetry we then have $$F(d)=\int_0^1 p(r)\>3r^2\>dr\ ,\tag{1}$$ because the variable $R:=|{\bf p}|$ has probability density $f_R(r)=3r^2$ $(0< r<1)$.

The following figure shows $B_1$ (centered at $0$) and the ball $B_d$ of radius $d$ (centered at ${\bf p}$). We can say that $$p_d(r)={{\rm vol}(B_d\cap B_1)\over{\rm vol}(B_1)}\ .\tag{2}$$

When $1-r<d<1+r$ the red and the black circles in the figure intersect. The intersection $B_d\cap B_1$ then is the union of two spherical caps $C_d$ and $C_1$. In order to obtain the volume of $C_d\cup C_1$ we have to determine the value of $z$ in the figure. This value comes from the two equations $$x^2+z^2=1,\qquad x^2+(z-r)^2=d^2\ ,$$ and is given by $$z={1+r^2-d^2\over 2r}\ .$$ According to the formula for $V^{(2)}$ in the given link we obtain $${\rm vol}(B_d\cap B_1)={\rm vol}(C_d\cup C_1) ={\pi\over3}\bigl((1-z)^2(2+z)+(z+d-r)^2(2d+r-z)\bigr)\ .$$ Dividing this by ${4\pi\over3}$, see $(2)$, gives $p_d(r)$. The result of the computation is $$p_d(r)= {-3+6d^2-3d^4\over 16}{1\over r}+{1+d^3\over2}-{3+3d^2\over8}r+{1\over16}r^3 \qquad(1-r<d<1+r)\ .$$ Assume $d\leq1$. When $d<1-r$, i.e., $r<1-d$, then $B_d\cap B_1=B_d$, so that $p_d(r)=d^3$. From $(1)$ it follows that $$F(d)=\int_0^{1-d}d^3\cdot 3r^2\>dr+\int_{1-d}^1p_d(r)\cdot3r^2\>dr=d^3-{9\over16}d^4+{1\over32}d^6\qquad(0\leq d\leq1)\ .\tag{3}$$ Similarly, assume that $d\geq1$. When $d>1+r$, i.e., $r<d-1$, then $B_d\cap B_1=B_1$, so that $p_d(r)=1$. It follows that $$F(d)=\int_0^{d-1}1\cdot 3r^2\>dr+\int_{d-1}^1p_d(r)\cdot3r^2\>dr=d^3-{9\over16}d^4+{1\over32}d^6\qquad(1\leq d\leq2)\ .\tag{4}$$ The formulas $(3)$ and $(4$) show that we have the clearcut result $$F(d)=d^3-{9\over16}d^4+{1\over32}d^6\qquad(0\leq d\leq2)\ .$$

Answer 2

Not a full answer, but a start...

Although the question doesn't state it, we must assume that the points are uniformly chosen within the volume of the sphere of radius $1$. The first point is at some radius $0 \leq r_1 \leq 1$, and we can choose our coordinates where that point lies on the $z$ axis. (Alternatively, we can, without loss of generality, rotate the sphere so that point 1 is on the $z$ axis.) Point 2 is at radius $0 \leq r_2 \leq 1$ at some azimuthal angle around the $z$ axis. We can, again without loss of generality, rotate our reference frame (or the sphere) so that point 2 lies in the plane $y=0$.

The origin and both points, then, lie in the plane $y=0$. Point 2 lies at some elevation angle $0 \leq \theta \leq \pi$.

The distance between these two points is then given by the law of cosines:

$$d = \sqrt{r_1^2 + r_2^2 - 2 r_1 r_2 \cos \theta}$$

Of course $0 \leq d \leq 2$.

Note that because of the densities of finding a given $r_i$ we have:

$$p(d) \propto \int\limits_{r_1=0}^1 dr_1 \int\limits_{r_2 = 0}^1 dr_2 \int\limits_{\theta = 0}^{\pi} d\theta \sqrt{r_1^2 + r_2^2 - 2 r_1 r_2 \cos \theta}\ p(r_1) p(r_2)$$

Here $p(r_i)$ is the probability of finding a point at a given radius, which because of the volume of a sphere is proportional to $r_i^2$. The full integral will surely involve elliptic integrals.

Once you get $p(d)$ for $0 \leq d \leq 2$, you can find the probability it is greater than some criterion $d_0$ by integration.

---

Because it was asked in a comment... yes, Mathematica:

Graphics3D[
 {Opacity[0.5], Sphere[],
  Yellow, InfinitePlane[{0, 0, 0}, {{1, 0, 0}, {0, 0, 1}}],
  Red, Opacity[1], Thickness[0.01], 
  Line[{{0, 0, 0}, {0, 0, .7}, {.3, 0, .5}, {0, 0, 0}}],
  Black, PointSize[0.03], Point[{0, 0, .7}], Point[{.3, 0, .5}], 
  Point[{0, 0, 0}],
  Text[Style["\[Theta]", 18], {.05, 0, .2}]},
 Boxed -> False]