Cauchy–Riemann Equations Intuition

Question

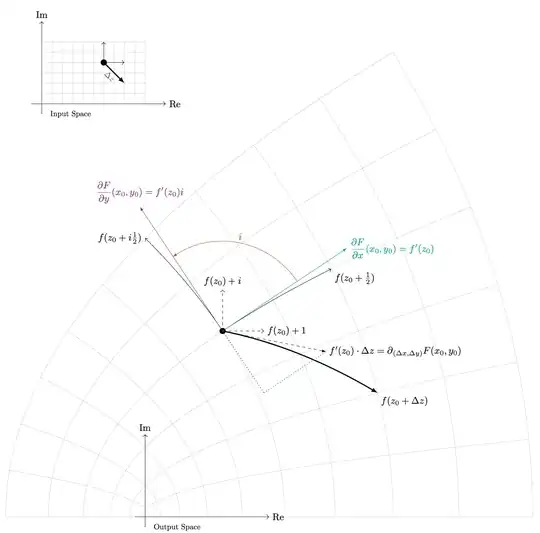
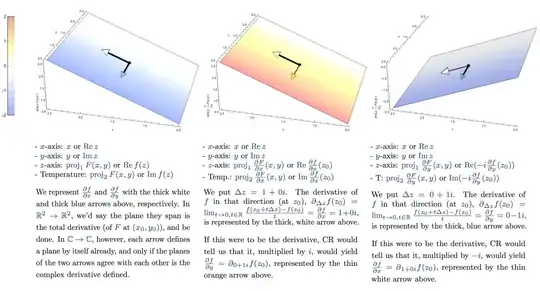
If $f(x + iy) = u(x,y) + i v(x,y)$, then $\frac{\partial f}{\partial x}$ describes how $f$ changes if we take take small step in the $x$-direction in the input space, and $\frac{\partial f}{\partial y}$ describes how $f$ changes if we take a small step in the $y$-direction in the input space.

I've been thinking of $f'(z_0)$ as the "guess" for how $f$ would change if we took the step $1+i0$ in the input space, since the guess is the derivative multiplied by the step. This, as is expected, coincides with how we expect $f$ to change when we move along the $x$-axis of the input space, i.e. $\frac{\partial f}{\partial x}$. Our guess for how $f$ would change if we took the step $0+i1$ in the input space would, similarly, coincide with $\frac{\partial f}{\partial y}$. Accordingly, $\frac{1}{i}\frac{\partial f}{\partial y}$ describes how $f$ changes if we took a step in the $(\frac{1}{i})(0+i1) = 1+i0$ direction in the input space. Except not necessarily? I mean, for this to hold the Cauchy–Riemann Equations have to be satisfied, right? (E.g. the last line wouldn't work for $\operatorname{Re}:\mathbb{C}\to\mathbb{C}$.) But why? Where have we used them in this line of argument?

Also, intuitively, why does $$ \lim_{h\to 0} \frac{ f(z_0 + ih) - f(z_0) }{ ih } $$ equal $$ \lim_{h\to 0} \frac{f(z_0 + h) - f(z_0)}{ h }, $$ or, say, what does it, intuitively, mean for them to be equal? (No matter how you approach $z_0$ the derivative $f'(z_0)$ must stay the same, sure, but, is there something more visual or basic that one could use as intuition?)

---

Edit: A visual for $f(z) = z^2$:

---

Edit 2: A different sort of visual, this time for $f(z)=\overline{z}$, with some text of me trying to understand it:

Answer 1

The most visual way of describing this is to return to the original geometric definition of differentiability: at $z_0$, the function has a unique tangent. The Cauchy-Riemann equations are a necessary condition for this geometric property.

Unfortunately it is not easy to draw a picture, because a function $\mathbb{C} \rightarrow \mathbb{C}$ is best visualized by thinking of $\mathbb{C}$ as a 2-dimensional real space, so the graph of the function would be in 4D.

If the function has a unique tangent plane, then the tangent vectors at $z_0$ all lie along this same plane, no matter which direction you take. The expression $$ \lim_{h \rightarrow 0} \frac{f(z_0 + ih) - f(z_0)}{ih} $$ is the difference quotient along the positive imaginary axis, like a complex analog to left and right derivatives. But these limits are all equal, then the full limit $$ \lim_{z \rightarrow z_0} \frac{f(z) - f(z_0)}{z - z_0}$$ becomes well-defined.

Answer 2

There are two ways to look at derivatives. One option is to consider a function at some point and to ask: if I take a tiny step away from this point, how does the function change? Another possibility is to ask: if I look at how the function transforms a tiny neighborhood of some point, can I find a linear map which transforms the neighborhood in the same way? In 1d real analysis, the former is more commonly used. But in multivariable analysis, the latter gives more insight, if you ask me. And complex analysis is basically a very special case of multivariable analysis (with two variables).

So in complex analysis, if the derivative of $f$ at $z_0$ is $f'(z_0)$, this means that in a tiny neighborhood of $z_0$ we have $f(z)\approx f(z_0)+f'(z_0)(z-z_0)$. This means that the way $f$ transforms that neighborhood is by first translating it to a neighborhood of $0$ ($z\mapsto z-z_0$), then multiplying every point by $f'(z_0)$ ($z\mapsto f'(z_0)(z-z_0)$), then translating to $f(z_0)$ ($z\mapsto f(z_0)+f'(z_0)(z-z_0)$). The relevant part is the multiplication by $f'(z_0)$, the translations are boring. Multiplication by a complex number is a rotation-dilation: if we multiply a complex number $z$ by the complex number $w$, we take the polar angle of $w$ and rotate $z$ by that amount, and then we take the modulus of $w$ and dilate $z$ by that amount. That's a rotation-dilation.

Now if we imagine $\mathbb C$ as $\mathbb R^2$, then we can notice that rotation dilations are linear and ask: what does the matrix representation of a rotation-dilation look like? And the answer is one of these: $$\begin{pmatrix}a&-b\\b&a\end{pmatrix},~r\begin{pmatrix}\cos\varphi&-\sin\varphi\\ \sin\varphi&\cos\varphi\end{pmatrix}.$$ The latter is just the former expressed in polar coordinates, where $r$ can be identified as the dilation factor and $\varphi$ as the rotation angle.

So as a real function, we have $f(x,y)\approx f(x_0,y_0)+A(x-x_0,y-y_0)$, where $A$ is a matrix of the form shown above. But that just means that $f$ is real differentiable with Jacobian $A$. And we know that the Jacobian contains the partial derivatives of the components $u,v$ of $f$. So on the one hand, the Jacobian is of the form $$\begin{pmatrix}u_x&u_y\\v_x&v_y\end{pmatrix}.$$ But on the other hand, it's also of the form $$\begin{pmatrix}a&-b\\b&a\end{pmatrix}.$$ Comparing all the entries of these matrices gives us the Cauchy-Riemann equations.

To recap: complex differentiable functions locally look like multiplication by a complex number, which is a rotation dilation. So their Jacobian must be the matrix representation of a rotation dilation. And since the Jacobian contains the partial derivatives, enforcing any condition on the Jacobian is the same as enforcing some condition on the partial derivatives. The condition "the Jacobian is a rotation-dilation" becomes "the partial derivatives satisfy the Cauchy-Riemann equations".