I need to use a central difference scheme:
$$\frac{dy}{dx}=\frac{y_{i+1}-y_{i-1}}{2 \Delta x}$$
equivalent for non centered point:
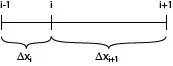
Unfortunately I cannot find a book in which I have this formula. Could anybody give me this in answer?
I need to use a central difference scheme:
$$\frac{dy}{dx}=\frac{y_{i+1}-y_{i-1}}{2 \Delta x}$$
equivalent for non centered point:

Unfortunately I cannot find a book in which I have this formula. Could anybody give me this in answer?
Actually you can use Taylor expansion to derive the formula $$y_{i-1}=y(x-\Delta x_i)=y(x)-\frac{dy}{dx}\Delta x_i+O(\Delta x^2)$$ $$y_{i+1}=y(x+\Delta x_{i+1})=y(x)+\frac{dy}{dx}\Delta x_{i+1}+O(\Delta x^2)$$ By neglecting higher order terms $O(\Delta x^2)$ $$y_{i+1}-y_{i-1}=\frac{dy}{dx}\Delta x_{i+1}+\frac{dy}{dx}\Delta x_i\Rightarrow \frac{dy}{dx}=\frac{y_{i+1}-y_{i-1}}{\Delta x_{i+1}+\Delta x_i}$$