Sketch of proof concerning a conjecture of Vasile Cirtoaje : $(1-x)^{(2x)^k}+x^{(2(1-x))^k}\leq 1$ with $k\geq1$ and $0

Question

Claim

Prove that [1]:

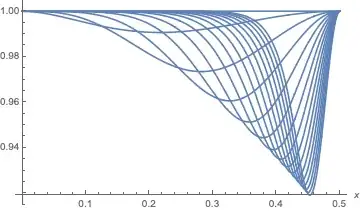
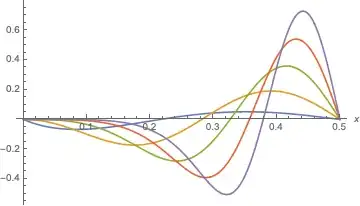
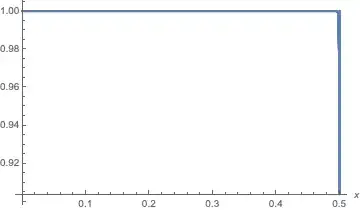
Let $0<x\leq 0.5$ and $k\geq 1$ a real number then we have :

$$h(k)=(1-x)^{(2x)^k}+x^{(2(1-x))^k}\leq 1$$

Sketch of proof :

The case $k\geq 1+\alpha$ :

We define $\alpha$ as :

$$\lim_{x\to 0.5^-}=\frac{\ln\Big(2(2^{2x}x^2(1-x)2)\Big)}{\ln(2x)}=\frac{\ln\Big(2(1-(2^{2x}x^2(1-x)2))\Big)}{\ln(2(1-x))}=\alpha=1.69315\cdots$$

We have :

$$x^{2(1-x)}\leq2^{2x}(1-x)2x^2$$

And :

$$(1-x)^{2x}\leq 1-2^{2x}(1-x)2x^2$$

For a sketch of proof see Refinements of the inequality $f(x)=x^{2(1-x)}+(1-x)^{2x}\leq 1$ for $0<x<0.5$

So we have :

$$x^{(2(1-x))^k}\leq f(x)^{(2(1-x))^{k-1}}=(2^{2x}(1-x)2x^2)^{(2(1-x))^{k-1}}$$

And :

$$(1-x)^{(2x)^k}\leq (1-2^{2x}(1-x)2x^2)^{(2x)^{k-1}}$$

Now we want $y\geq 1$ a real number :

$$(2x)^{k-1}\geq (2f(x))^{y}$$ And $$(2(1-x))^{k-1}\geq (2(1-f(x)))^{y}$$

Solving this we have

$$\frac{\ln\Big(2(1-(2^{2x}x^2(1-x)2))\Big)}{\ln(2(1-x))}\leq \frac{k-1}{y}\leq \frac{\ln\Big(2(2^{2x}x^2(1-x)2)\Big)}{\ln(2x)}\quad (1)$$

The constraint $(1)$ is honoured if :$$\alpha=\frac{k-1}{y}$$

So we have :

$$x^{(2(1-x))^k}\leq (f(x))^{(2(1-f(x))^{\frac{k-1}{\alpha}} }\quad (2)$$

And :

$$(1-x)^{(2x)^k}\leq (1-f(x))^{(2f(x))^{\frac{k-1}{\alpha}}}\quad (3)$$

Adding $(2)$ and $(3)$ we have :

$$h(k)\leq (1-f(x))^{(2f(x))^{\frac{k-1}{\alpha}}}+(f(x))^{(2(1-f(x))^{\frac{k-1}{\alpha}}}$$

We can repeat the reasoning $p$ times ($p\geq 1$ a natural number) and the last exponent becomes :

$$1\leq \frac{k-1}{\alpha^p}\leq \alpha$$

It's true because we can always choose $k$ such that :

$$\alpha^p\leq k \leq \alpha^{p+1}$$

So we reduce this case to the case $1\leq k\leq 1+\alpha $

Case $k\leq 1+\alpha $

Using Bernoulli's inequality and derivatives we have $1\leq k\leq 2$ and $0<x\leq \frac{1}{4}$

$$(1-x)^{(2x)^k}\leq 1-x(2x)^k$$ And $$x^{(2(1-x))^k}\leq x(2x)^k$$

In the same idea we have $2\leq k\leq 1+\alpha$ and $0<x\leq \frac{1}{3}$

$$(1-x)^{(2x)^k}\leq 1-x(2x)^k$$ And $$x^{(2(1-x))^k}\leq x(2x)^k$$

Now to finalize the sketch of proof we have :

$h(k)$ is decreasing for $1\leq k\leq 2$ and $ \frac{1}{4}\leq x\leq 0.5\quad (4)$

$h(k)$ is decreasing for $2\leq k\leq 1+\alpha$ and $ \frac{1}{3}\leq x\leq 0.5\quad (5)$

Questions :

It is good and coherent ?

How to show $(4)$ and $(5)$?

Thanks in advance !

Regards Max

[1] Vasile Cirtoaje, "Proofs of three open inequalities with power-exponential functions", The Journal of Nonlinear Sciences and its Applications (2011), Volume: 4, Issue: 2, page 130-137. https://eudml.org/doc/223938

https://link.springer.com/article/10.1186/1029-242X-2013-468

Answer 1

I prefer to do this this analytical process.

Look at the function with lower k:

I mathematica it is often sensible to look at the function sequence on the borders of the interval of interest. In this case it is possible to state this values for all k. $f(0)=1$ and $f(0.5)=0$. Inbetween the function can either be bigger or smaller than $1$. The functions are polynoms in x, so monomials, but with mixed order. So they are steady and differentiable on the interval and the boundary. There positive as well as negative. But both terms are positive on the interval for all k $1>0.5>x>0$.

There must be for each k a global unique minimum or maximum. This property decides whether the function are bigger or smaller than $1$ in the interval $(0,0.5)$.

The first derivative looks even as nice as the function:

This few derivative show the beauty and complexity of the derivatives in full.

$$(1 - x)^(2^k x^ k) (-((2^k x^k)/(1 - x)) + 2^k k x^(-1 + k) Log[1 - x]) + x^(2^k (1 - x)^k) ((2^k (1 - x)^k)/x - 2^k k (1 - x)^(-1 + k) Log[x])$$

Because this already has the logarithm function combined with the polynomials it is not solvable in a closed form.

With numerical methods it is easy to find the zeros of the functions sequence. It starts with

$${0.216454, 0.281732, 0.326587, 0.357129, 0.378871, 0.395017, \ 0.407435, 0.417264, 0.425226}$$

What we need for a prove is only that there is one for shure for all k.

All these function value at the extrema are smaller than $1$.

$${0.990665, 0.973494, 0.960633, 0.951346, 0.944465, 0.939202, \ 0.935062, 0.931727, 0.928985}$$

This is in the start already a continuously falling sequence. Since these are polynomial this will continue for all k. At that is the prove with the methods of numerics and analysis.

$$\lim_{k\rightarrow\infty}f(x_{Extrema,k})=0$$

with

$$\lim_{k\rightarrow\infty}x_{Extrema,k}=0.5$$

Therefore the

$(1−)^{(2)^}+^{(2(1−))^}≤1$ with $≥1$ and $0<≤\frac{1}{2}$ and $k$ natural

ist true.

$\lim_{k\rightarrow\infty}(1−)^{(2)^}+^{(2(1−))^}=1$ if $\log(1 - x) < -\log(2)$ $and$ $\log(x) > -\log(2)]$

So the function sequence converges pointwise towards 1, but remains the extrema which is proven as a global unique minimum but the minimun converges to 0.5. The limit therefore is constant $1$.

These can be interpreted as a sum of two sequences. The first one is the same as the second one if 1-x=t and 0.5<t<1. So the first part increases with k to 1 and the second to 0 with k. Like the functions sequence $x^k$ converges to 0 on $(0,1)$ converges this functions sequence to $1$. $x^k$ converges pointwise and global on $(0,1)$. The function sequence (1−)^{(2)^}+^{(2(1−))^} just converges pointwise on $(0,0.5)$. The global minimum on $(0,0.5)$ converges to $0.5$ and $1$ from below.

Answer 2

I have a second sketch/Partial proof (tell me if i'm wrong) :

We want to show

Let $0.65\leq x<1$ and $1\leq k\leq n$ two naturals numbers with $n\geq 10^{10}$ then we have ::

$$P(k)=(1-x)^{(2x)^{1+\frac{k}{n}}}+x^{(2(1-x))^{1+\frac{k}{n}}}\leq 1\quad (I)$$

We use a form of the Young's inequality or weighted Am-Gm :

Let $a,b>0$ and $0<v<1$ then we have :

$$av+b(1-v)\geq a^vb^{1-v}$$

Taking account of this theorem and putting :

$a=(x)^{(2(1-x))^{1+\frac{k}{n}}}$$\quad$$b=1$$\quad$$v=(2(1-x))^{\frac{1}{n}}$ we get :

$$(x)^{(2(1-x))^{1+\frac{k}{n}}}\leq (x)^{(2(1-x))^{1+\frac{k-1}{n}}}(2(1-x))^{\frac{1}{n}}+1-(2(1-x))^{\frac{1}{n}}$$

Now the idea is to show :

Let $$(1-x)^{(2x)^{1+\frac{k}{n}}}\leq 1-\Big((x)^{(2(1-x))^{1+\frac{k-1}{n}}}(2(1-x))^{\frac{1}{n}}+1-(2(1-x))^{\frac{1}{n}}\Big)$$

Or: $$(1-x)^{(2x)^{1+\frac{k}{n}}-\frac{1}{n}}+2^{\frac{1}{n}}(x)^{(2(1-x))^{1+\frac{k-1}{n}}}\leq 2^{\frac{1}{n}}\quad (0)$$

Now we have $x\in[0.65,1)$ :

$$2^{\frac{1}{n}}(1-x)^{(2(1-x))^{1+\frac{k-1}{n}}}\geq (1-x)^{(2(x))^{1+\frac{k}{n}}-\frac{1}{n}}\quad(1)$$

Putting $(1)$ into $(0)$ we can use a proof by induction and conlude with Refinements of the inequality $f(x)=x^{2(1-x)}+(1-x)^{2x}\leq 1$ for $0<x<0.5$

Edit :

Now I can complete it :

The problem can be considered as :

$$r(x)=\left((1-x)^{-\left(2\left(x\right)\right)^{k}}-1\right)\left((x)^{-\left(2\left(1-x\right)\right)^{k}}-1\right)\geq1$$

Lemma

Let $1< x$ and $a>2$ then we have :

$$f(x)=\left(1+\frac{\left(\ln\left(ax\right)^{c}-\ln\left(a\right)^{c}\right)}{\left(\ln\left(2a\right)^{c}-\ln\left(a\right)^{c}\right)}-x\right)\leq 0$$

We can find $c$ as $f'(2)=0$.The definition of $c$ involves the Lambert's function.

Proof :

We have :

$$f'(x)=\frac{c(\ln(ax))^{c-1}}{x\left(\ln\left(2a\right)^{c}-\ln\left(a\right)^{c}\right)}-1$$

We substitute $x=\frac{1}{y^{c-1}a}$

The inequality have the form :

$$\ln(u)u=p$$

Wich is just the Lambert's function . The rest is easy .

End of the proof .

Now we apply twice the second lemma and we start by introducing (see the reference) :

$$f(x)=((\ln((a)b^{-(2(1-b))^x}))^c-(\ln(a))^c) ((\ln((a)(1-b)^{-(2(b))^x}))^c-(\ln(a))^c)$$

The derivative is :

$$f'(x)=c(u(x)+v(x))$$

Where :

$$u(x)=\left(2-2b\right)^{x}\cdot\ln(2\left(1-b)\right)\cdot\ln(b)\cdot\left((\ln(a))^{c}-\left(\ln(a\cdot\left(1-b\right)^{-(2b)^{x}})\right)^{c}\right)\left(\ln(a\cdot(b)^{-\left(2-2b\right)^{x}})\right)^{\left(c-1\right)}$$

$$v(x)=2^{x}\cdot b^{x}\cdot\ln(1-b)\cdot\ln(2b)\cdot\left((\ln(a))^{c}-\left(\ln(a\cdot b^{-(2-2b)^{x}})\right)^{c}\right)\left(\ln(a\cdot(1-b)^{-2^{x}b^{x}})\right)^{\left(c-1\right)}$$

A bit of Algebra and we need to show something like:

$$\frac{\left(2-2b\right)^{x}\cdot\ln(2\left(1-b)\right)\cdot\ln(b)}{2^{x}\cdot b^{x}\cdot\ln(1-b)\cdot\ln(2b)}\geq^{?}-\left(\frac{\left((\ln(a))^{c}-\left(\ln(a\cdot\left(1-b\right)^{-(2b)^{x}})\right)^{c}\right)\left(\ln(a\cdot(b)^{-\left(2-2b\right)^{x}})\right)^{\left(c-1\right)}}{\left((\ln(a))^{c}-\left(\ln(a\cdot b^{-(2-2b)^{x}})\right)^{c}\right)\left(\ln(a\cdot(1-b)^{-2^{x}b^{x}})\right)^{\left(c-1\right)}}\right)^{-1}\quad(U)$$

We can split in two the problem as :

$$\left(\frac{\left((\ln(a))^{c}-\left(\ln(a\cdot\left(1-b\right)^{-(2b)^{x}})\right)^{c}\right)}{\left((\ln(a))^{c}-\left(\ln(a\cdot b^{-(2-2b)^{x}})\right)^{c}\right)}\right)^{-1}\geq^{?}\frac{\left(\left(2-2b\right)^{x}\right)^{\left(1+v\right)}\cdot\ln(b)}{\left(2^{x}\cdot b^{x}\right)^{\left(1+w\right)}\cdot\ln(1-b)}$$

And :

$$-\left(\frac{\left(\ln(a\cdot(b)^{-\left(2-2b\right)^{x}})\right)^{\left(c-1\right)}}{\left(\ln(a\cdot(1-b)^{-2^{x}b^{x}})\right)^{\left(c-1\right)}}\right)^{-1}\leq^{?}\frac{\left(\left(2-2b\right)^{x}\right)^{\left(-v\right)}\cdot\ln(2-2b)}{\left(2^{x}\cdot b^{x}\right)^{\left(-w\right)}\cdot\ln(2b)}$$

With $v,w>0$

It works for small values so it's perfect for $1\leq k\leq 3$ and $a$ sufficiently big and $0.5\leq x\leq0.75$ .

I pursue it later .

Vasile Cirtoaje, "Proofs of three open inequalities with power-exponential functions",

The Journal of Nonlinear Sciences and its Applications (2011), Volume: 4, Issue: 2, page 130-137. https://eudml.org/doc/223938

Miyagi, M., Nishizawa, Y. Proof of an open inequality with double power-exponential functions. J Inequal Appl 2013,

https://link.springer.com/article/10.1186/1029-242X-2013-468