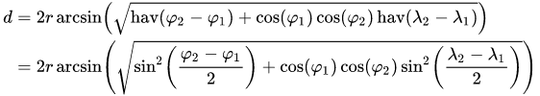1

As an aviator I'm familiar with the concept of great-circle navigation because when we fly a route between 2 points on the globe we know the shortest distance between these two points is the great circle distance.

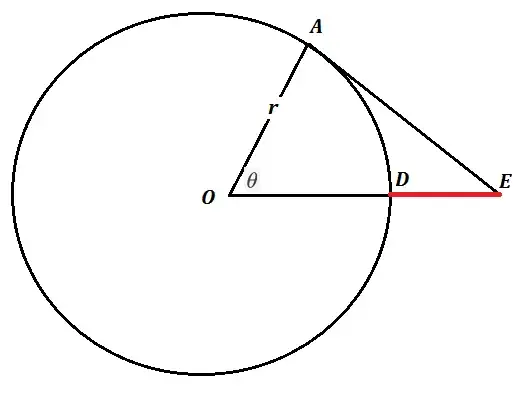
I'm developing a navigation app in Google Earth and I need to calculate the shortest distance from the surface of the "spherical" Earth to any point on the tangent line through A (origin) when flying the great circle path.

Also, I'm using a mean earth radius of 6,371.009 km for WGS84 ellipsoid.

Just to be clear, I'd like to refer to the diagram in the following link:

http://www.alaricstephen.com/main-featured/2017/5/22/the-haversine-formula

I use the Haversine formula to calculate the distance, d, between the points A and D (see diagram). What I'd like to calculate is the distance D to E as a function of d.

In the diagram this is referred to as the external secant (exsec) which is the portion DE of the secant exterior to the circle.

rgraulus
  • 13
  • Do you have a figure? – Shubham Johri Oct 30 '20 at 22:40
  • I rephrased my question referring to a diagram I found in the following link http://www.alaricstephen.com/main-featured/2017/5/22/the-haversine-formula – rgraulus Oct 31 '20 at 15:52
  • 1
    The tangent line from a point is not unique. If you mean the tangent line in the plane of the great circle, then your problem is a planar one and you don't need any spherical trigonometry. Now it is unclear if you use a spherical or ellipsoidal model. –  Oct 31 '20 at 16:22
  • 1
    That diagram uses a unit circle, and it says that the distance ED is $\sec\theta-1$. – PM 2Ring Oct 31 '20 at 16:31
  • If you would like to use an ellipsoidal model, take a look at Charles Karney's free geographiclib. FWIW, Dr Karney is a major contributor to the Wikipedia articles on ellipsoidal navigation. geographiclib is written in C++, but with bindings available in many languages. Karney's algorithms always converge (unlike the old Vincenty algos), and whereas Vincenty can often give errors of a metre or more, the error from Karney's algorithms are on the order of a nanometre, when used on the WGS84 ellipsoid. – PM 2Ring Oct 31 '20 at 16:54

2 Answers2

2

$$r=OE\cos\theta$$

and

$$DE=r\sec\frac{\stackrel\frown{AD}}r-r.$$

  • Yes, I do mean the tangent line in the plane of the great circle. To calculate DE, I assume a circle with mean radius r which will have some error knowing that Google Earth is WGS84 ellipsoid. – rgraulus Oct 31 '20 at 17:17
  • @rgraulus: then my formula holds. –  Oct 31 '20 at 17:37
1

HaverSine Formula is used routinely to compute long distances in navigation along shortest path great circles of the Earth between two points of given latitude and longitude.

enter image description here

First find $d$ on the Earth. Next air distance along a tangent if the flight point $B$ is above the Earth: $ t= r \tan \dfrac{d}{r}.$

$-------------------------$

After clarification the above can be ignored.

For perfect sphere model of earth it is simple trig. calculation.

Distance $ AD= r \theta = $ the arc distance you calculated using Haversine formula along a great circle arc of earth radius $=r$ as shown. Calculate $ \theta $ in radians in the plane of kite shape $OAEB$ if we imagine $B$ on another tangent point below. We have $ \theta= \dfrac{\text{arc} AD}{r}$

enter image description here

Central dimension is length $OE$. From this subtract earth radius.

$$ DE = r \sec \theta - r\; = r (\sec \theta -1 )$$

This is the red height above target/destination/landing place which should vanish on landing at $D$. It is indicated by exsec in the supplied link for unit earth radius.

Narasimham
  • 40,495