Trigonometric equation $1-\frac{1}{\sin(x)}-\frac {1}{\cos(x)}=0$

Question

The equation is $$1-\frac{1}{\sin(x)}-\frac {1}{\cos(x)}=0$$ I have tried multiplying both sides by $\sin(x)\cos(x)$ and I got $$\sin(x)\cos(x)-\cos(x)-\sin(x)=0$$ but honestly I think the only way out here is by a graph?

Answer 1

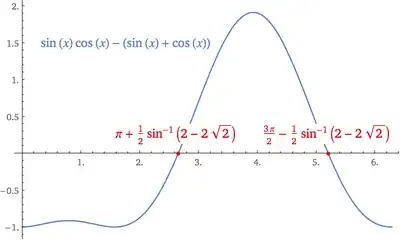
Multiply by $\sin(x)\cos(x)$: $$ \sin(x)\cos(x)=\sin(x)+\cos(x)\tag1 $$ Square and multiply by $4$: $$ 4\sin^2(x)\cos^2(x)=4+8\sin(x)\cos(x)\tag2 $$ Apply $\sin(2x)=2\sin(x)\cos(x)$: $$ \sin^2(2x)-4\sin(2x)-4=0\tag3 $$ Solve: $$ \sin(2x)=2-2\sqrt2\tag4 $$ Since $2+2\sqrt2\gt1$, we don't want that solution.

$(4)$ yields the $4$ possible solutions: $$ \scriptsize x\in\left\{\color{#AAA}{\frac12\sin^{-1}\left(2-2\sqrt2\right),\frac\pi2-\frac12\sin^{-1}\left(2-2\sqrt2\right),}\pi+\frac12\sin^{-1}\left(2-2\sqrt2\right),\frac{3\pi}2-\frac12\sin^{-1}\left(2-2\sqrt2\right)\right\}\tag5 $$ Note that $x\mapsto\pi+x$ negates $\sin(x)+\cos(x)$ but leaves $\sin(x)\cos(x)$ unchanged. Thus, each solution will have a non-solution offset by $\pi$.

The first two solutions in $(5)$ give $\sin(x)\cos(x)=-\sin(x)-\cos(x)$, so we only want the last two solutions.

Answer 2

Hint:

If $\sin x+\cos x=y,$

$ y^2=?,$

$-\sqrt2\le y\le\sqrt2\ \ \ \ (1)$

$$\dfrac{y^2-1}2=y\iff y^2-2y-1=0\iff(y-1)^2=2$$

$\implies y=1\pm\sqrt2$

By $(1), y\ne1+\sqrt2$

Answer 3

Apply the half-angle substitution $t= \cot \frac x2$ to $1-\frac{1}{\sin x}-\frac {1}{\cos x}=0$ $$t^4+ 4t -1=0$$ which factorizes as

$$(t^2+2a t+\frac{2a^3-1}a)(t^2-2a t+\frac{2a^3+1}a)=0$$ with $a^6+\frac14a^2-\frac14=0$, which yields $a^2=\frac12$. Plug it into above equation to obtain a pair of real roots $$t=\frac{-1\pm\sqrt{2\sqrt2-1}}{\sqrt2}$$ Thus, the solutions for $x$ are $$x=2n\pi+2\cot^{-1} \frac{-1\pm\sqrt{2\sqrt2-1}}{\sqrt2} $$

Answer 4

$$\sin(x)\cos(x)=\sin(x)+\cos(x)$$ $$\frac12 (\sin(2x))=\sin(x)+\cos(x)$$ $$\frac{\sin(2x)}{2}=\sin(x)+\cos(x)$$ $$\frac12 (\sin(2x))=\frac{2}{\sqrt2}(\sin(x+\frac{π}{4}))$$ $$\sin(2x)=\frac{4}{\sqrt2}\left(\sin(x+\frac{\pi}{4}) \right)$$ $$\sin(2x)=2\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)$$ $$2\sin^2\left(x+\frac{π}{4}\right)-1=2\sqrt{2}\sin\left(x+\frac{π}{4}\right)$$ $$2\sin^2\left(x+\frac{π}{4}\right)-1-2\sqrt{2}\sin\left(x+\frac{π}{4}\right)=0$$ $$2{\color{green}{\sin^2\left(x+\frac{π}{4}\right)}}-2\sqrt2 {\color{green}{\sin\left(x+\frac{π}{4}\right)}}-1=0$$