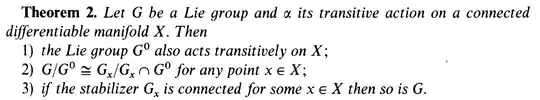G_x\cap G^0$

Asked Nov 25 '20 at 05:30

Active Nov 25 '20 at 05:30

Viewed 39 times

I have difficulties prove and understanding the second statement of this theorem. I tried to construct the homomorphism $$\varphi:G_x\to G/G^0$$ given by $\varphi(g)=gG^0$ where $G^0$ is a connected component of the identity $e$ in $G$ i.e. $G^0$ is normal in $G$. I can show that $ker(\varphi)=G_x\cap G_0$. But, how do I show that $\varphi$ is surjective?

asked Nov 25 '20 at 05:30

user89898989

2

You are trying to prove that $G_xG^0=G$, which is equivalent to $G^0$ acting transitively on $X$, which is the topic of this question – Derek Holt Nov 25 '20 at 08:48
@DerekHolt Thank you! – user89898989 Nov 25 '20 at 18:25

Help with understanding this Theorem: $G/G^0\cong G_x/G_x\cap G^0$

0 Answers0