Geometrically, why are complex numbers both linear maps that perform rotation/dilation, and points on the plane?

Question

The standard geometric interpretation of complex numbers is to draw the complex plane by identifying the horizontal axis as the real axis and the vertical axis as the imaginary axis, so that the complex number $z = x + iy$ is identified with the point $(x, y)$. That is to say, a complex number is geometrically a point on the plane.

But we also know from the polar form of complex numbers that when we multiply two complex numbers $z=r(\cos \alpha + i \sin \alpha)$ and $w=s(\cos \beta + i \sin \beta)$ that we can “add the angles and multiply the distances” to get $zw=rs(\cos(\alpha + \beta) + i \sin(\alpha + \beta))$. That means we can view one of the complex numbers, say $z$, as being a linear map that performs a rotation and/or dilation on the other number (here $w$) which is viewed as a point, to return a new point.

In linear algebra though, a point is a vector $v \in V$, and a linear map is a function $T: V \to W$. These are two different kinds of objects, and it would be a type error to try to identify $v$ with $T$ somehow. So my question is something like, why does it work out that complex numbers can be viewed in two different ways even though that seems like a type error?

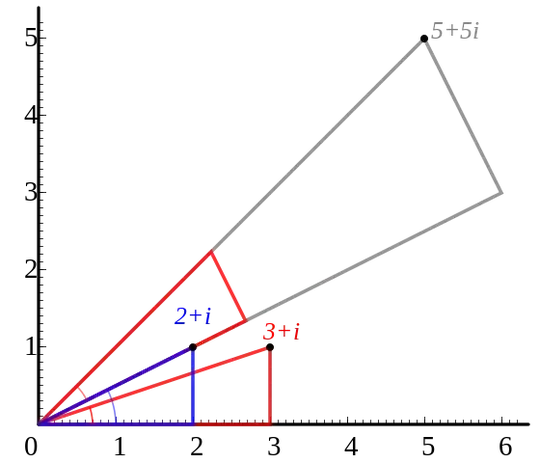
If I stopped here though I feel like people would just give me examples of other things in math where it's possible to view a single object through multiple geometric "lenses". (Maybe that is what I want, but I feel like there is still something to my original question.) So let me go a little further: Of course there are many situations where the same objects can be visually represented in different ways, e.g. a real number can be both a length and an area and a volume and so forth. And even in the case of real numbers, we can say that we start with some distance $x$, then multiply by a distance $y$ to get a distance $yx$. In that case, isn’t $y$ acting as a “linear map” $x \mapsto yx : \mathbf R \to \mathbf R$? That’s true, but we can also use similar triangles (figure from this book, p. 3) to show that $y$ can be seen as a length as well, so that $x$, $y$, and $yx$ are all lengths in a single figure. It’s this extra step that seems to be missing from the case of complex number multiplication.

Answer 1

Perhaps a slight change of perspective could prove useful: we think of complex numbers just as that, points in the complex plane. However, we can prove that the functions which just multiply by some fixed complex number

$f_c: \mathbb{C} \to \mathbb{C}, f_c(z) := cz$

are exactly all of the linear maps which perform rotation and dilation. Since every such function arises from exactly one $c \in \mathbb{C}$ and vice versa, it's natural to identify them (rather than directly defining complex numbers as being these maps). So the solution to this "type error" (which I think is a nice way to put it) is that we do indeed have two different sets (the set of vectors in the complex plane, and the set of maps as already described) which just happen to be very naturally bijective.

Answer 2

Because real-number arithmetic is "rectangle arithmetic", and complex-number arithmetic is "circle arithmetic", in some sense. Take two points on the plane... say, $(a,b)$ and $(c,d)$. You want to do arithmetic between these two points. The obvious candidate for addition and multiplication is to just add/multiply "element-wise", e.g. $(ac, bd)$. The arithmetic thus defined is also useful, but...

It turns out that the following operation: $(a,b)\cdot(c,d) = (ac - bd, ad + bc)$ behaves a lot like what we call "multiplication" in real numbers, so we go ahead and call it "multiplication" in our arithmetic between points on a plane. It turns out that this operation that we're calling "multiplication" between two pairs of points has a nice geometric interpretation in terms of rotations and dilations between Cartesian points on a plane $(a,b)$ and $(c,d)$:

All of the difference in interpretation you are curious about boils down to this definition of "multiplication": $(a,b)\cdot(c,d) = (ac - bd, ad + bc)$ It is the "rotation, dilation".

Answer 3

$ \newcommand\Cl{\mathrm{Cl}} \newcommand\R{\mathbb R} $Here is an answer which I hope isn't too algebraic for your taste.

The complex numbers are, algebraically, the Clifford algebra $\Cl_{0,1}(\R)$, but this is not what we are immediately interested in. What we are more interested in is $\Cl_2(\R)$, the Clifford algebra of 2D Euclidean space. Canonically, $\R^2 \subset \Cl_2(\R)$, and in fact $\Cl_2(\R)$ is generated by $\R^2$ as an algebra. The Clifford algebra is the the natural setting in which to study orthogonal transformations; a reflection through the hyperplane orthogonal to $v \in \R^2$ is given exactly by $x \mapsto -v^{-1}xv$, so by Cartan-Dieudonné all orthogonal transformations are represented by products of vectors acting similarly. The group $$ \mathrm{Pin}(2) = \{v_1\dotsb v_k \;:\; v_1^2\dotsb v_k^2 = 1,\: k \in \mathbb N\}, $$ called the pin group, is the double cover of $\mathrm O(2)$; if we remove the normalization condition, then we get the Lipschitz group $\Gamma(2) \supset \mathrm{Pin}(2)$. In particular, rotations are represented by products of an even number of vectors; in fact, all elements of $\Cl_2(\R)$ which are sums of products of an even number of vectors together form the even subalgebra $\Cl^+_2(\R)$. The subgroup of $\mathrm{Pin}(2)$ which is the double cover of $\mathrm{SO}(2)$ is the spin group: $$ \mathrm{Spin}(2) = \mathrm{Pin}(2)\cap\Cl^+_2(\R). $$ It turns out that the corresponding even Lipschitz group $\Gamma^+(2) = \Gamma\cap\Cl^+_2(\R)$ is in fact equal to $\Cl^+_2(\R)$; this will be important shortly.

Where the magic relevant to us starts happening is with $\Cl^+_2(\R)$; remember that I said this is a subalgebra, and in fact it is itself always a Clifford algebra: $$ \Cl^+_2(\R) \cong \Cl_{0,1}(\R) \cong \mathbb C. $$ This isomorphism depends on a choice of vector $r \in \R^2$, which we will assume is a unit vector so that $r^2 = 1$, and complete this to an orthonormal basis $\{r, r'\}$. For any $ar + br' \in \R^2$ we see $$ rv = r(ar + br') = a + brr'. $$ The "vectors" of $V^+ \subset \Cl^+_2(\R)$ are the non-scalar part $\{brr' \;:\; b \in \R\}$ of $rv$, and $V^+$ generates $\Cl^+_2(\R) \cong \Cl_{0,1}(\R)$. But notice we also naturally got an embedding of $\R^2$ into $\Cl^+_2(\R)$ via the map $v \mapsto rv$. These quantities, a sum of a scalar and a vector, are called paravectors, and it is easy to see in this case all elements of $\Cl^+_2(\R)$ are paravectors; of course we just described the real (scalar) and imaginary (non-scalar) part of complex numbers! Our choice of $r$ is exactly a choice of real axis in $\mathbb C$, and $i = rr'$ is the imaginary unit.

Now recall that $\Cl^+_2(\R) = \Gamma^+(2)$, so in particular a unit complex number $z$ is an element of $\mathrm{Spin}(2)$ and performs a rotation on vectors via $$ v \in \R^2 \mapsto v' = \widetilde zvz $$ where $\widetilde z$ can just be thought of as the conjugate (and I have not explained why the conjugation is necessary, but it is naturally part of how spin groups work). But we can translate this into an action on the paravectors of $\Cl^+_2(\R)$! using the fact that $r\widetilde z = zr$ and the complex numbers are commutative, we see $$ rv' = r\widetilde zvz = zrvz = z^2(rv). $$ So a complex number $z$ as an element of $\mathrm{Spin}(2)$ rotates elements of $\R^2$ thought of as paravectors via $w \mapsto z^2w$. It turns out that if $z$ is a rotation by $\theta$ then $z = e^{\theta rr'/2}$, so $$ w \mapsto e^{\theta rr'}w = e^{\theta i}w, $$ as we should expect.

---

For a more general and detailed discussion of paravectors, and the relation to both complex numbers and quaternions, please see my answer here.