3

How many factors of $2n^2$ are less than or equal to $n$? I know that the number of factors of $n^2$ less than $n$ is half the number of factors of $n^2$ (each factor $< n$ corresponds with one greater than $n$), but $2n^2$ is a whole different case, it seems. Is there any way to find an expression for this? And if not, is there an algorithm for it? I have looked into both combinatorics and prime factorization, but have arrived at dead-ends.

Déjà vu
  • 934
Han Xiong
  • 68
  • 8
  • The factors of $2n^2$ are $1, 2, n, 2n, n^2, $ and $2n^2$. – J. W. Tanner Dec 11 '20 at 04:35
  • 2
    No, those are the only "sure" factors that we know. For example, 2*15^2 = 450 is also divisible by 5, 18, and 25, to name a few. – Han Xiong Dec 11 '20 at 04:38
  • @J.W.Tanner: I think OP is considering the case where $n$ is composite. For example, $450=2\cdot 15^2$ has $18$ factors, $8$ of which are less than or equal to $15$. – Ross Millikan Dec 11 '20 at 04:38
  • 1
    @Han: there isn't an easy way to answer this without knowing the prime factorization of $n$. Unlike the $n^2$ case there isn't a neat trick. – Qiaochu Yuan Dec 11 '20 at 04:38
  • I do know the prime factorization of n, I'm trying to write a program for this. (Project Euler) – Han Xiong Dec 11 '20 at 04:39
  • Also to get the num. of factors in the first place, I would have to know the prime factorization. – Han Xiong Dec 11 '20 at 04:41
  • Which number is it (Project Euler)? – Déjà vu Dec 11 '20 at 04:43
  • https://projecteuler.net/problem=735, but that’s not really relevant here. – Han Xiong Dec 11 '20 at 04:47
  • There are straightforward algorithms for solving this given a particular value of $n$, of course. But I don't see any direct solution in the general case, as it seems to depend crucially upon the prime factorization of $n$. – David G. Stork Dec 11 '20 at 04:49

2 Answers2

2

This is a very interesting question. Assume $n=2^{a}(2k+1)$ for some integer $a$ and $k$. Let $f(x)=$numbers of positive divisors of the integer $x$ . Since factors of $2n^2\leq n$ we need number of factors of $2^{2a+1}(2k+1)^2$. Thus we have $f(2^a(2k+1))+c_{a}$.Where $c_{a}$ is the error factor has a small factor of bound, which needs to be deterministic. Although it's a rough idea, I am not finding the bound but for hints, you can try small cases. However let $g(x)=$greatest integer lesser equal to x then, $$c_{a}\leq f(g(2^{\frac{2a+1}{2}}(2k+1)))-f(2^a(2k+1))$$.Where we know $f$ is famous divisor function or $\tau$ function and $g$ is the floor function. Use this link for bound, Lower bound for the sum of divisor function

1

I see no general analytic solution, since it would seem to depend upon the prime factorization of $n$.

But the OP also asks for code. That is very straightforward. In Mathematica:

myfun[n_: Integer] := Length[
Select[Divisors[2 n^2], # <= n &]]

So:

myfun[9098345]

(* 27 *)

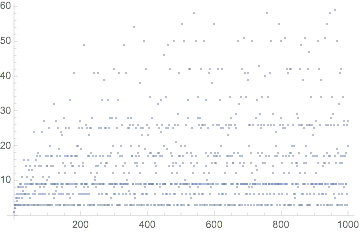
Here's a plot:

enter image description here

This isn't directly part of the problem, but seems to be the motivation of the problem. If the above function is $f(n)$, calculate $F(N) = \sum\limits_{n=1}^N f(n)$, for $N = 10^{12}$.

I think the approach is the following: Calculate the number of $2$s in that sum. Then calculate the number of $3$s. And so on, then add them up.

The number of $2$s is $10^{12}/2$. The number of $3$s is $10^{12}/3$. And so on. But what is the maximum we add those up to in the total calculation? I think it should be the largest factor allowed in the $10^{12}$ (last) term in the sum, i.e., $k_{max} = \sqrt{50} \cdot 10^5 = 707107$, obtained from the $2 n^2 = 10^{12}$ calculation.

If that's right, then: $F(10^{12}) = 10^{12} \sum\limits_{k = 1}^{k_{max}} \frac{1}{k} = 10^{12}\ {\rm HarmonicNumber}(k_{max}) = 10^{12} \cdot 14.0461536491411$.

There are probably some rounding artifacts that must be included, but I think this is the right approach. Someone should do this with greater care.

David G. Stork
  • 29,774
  • Just curiosity (based on the project Euler problem), how much time does it take to calculate for $n=10^{12}$ ? (the problem actually asks the sum of divisors for $n=1$ to $10^{12}$... only 95 people have been able to answer so far!) – Déjà vu Dec 11 '20 at 05:01
  • 1
    I do have one question: Exactly how efficient is this? (Time complexity wise) it looks like you’re just picking the divisors out that are <= n – Han Xiong Dec 11 '20 at 05:01
  • The time to compute myfun[10^(12)] is $0.000721$ seconds on a Mac laptop. – David G. Stork Dec 11 '20 at 05:26
  • Wow, is Mathematica really that fast? Thanks. – Han Xiong Dec 11 '20 at 05:29
  • Factoring composites is not a hard computational problem, but yes... Mathematica is highly optimized for number theoretic functions. I ran the first $10^6$ without smart re-use of calculations and it took $73$ seconds. On a multiprocessor this highly parallel computation would be much faster. – David G. Stork Dec 11 '20 at 05:31
  • Wow! You should be able to answer the problem within a reasonable time (sum of yourfun from $1$ to $10^{12}$), the calculation should be much faster for $10^{10}$ (for instance) – Déjà vu Dec 11 '20 at 05:32
  • You want the sum of the myfun?? – David G. Stork Dec 11 '20 at 05:33
  • Not me, if you want to answer the problem... – Déjà vu Dec 11 '20 at 05:34
  • 1
    Even though I see no analytic simplification for a single $f(n)$ (i.e., myfun), the ProjectEuler task is a bit different. It seeks $F(N) = \sum\limits_{n=1}^N f(n)$, with $N = 10^{12}$. I think the trick here is to find out how many $2$s will appear in this big sum. Then how many $3$s. Then how many $4$s, and so on. I don't have a solution approach beyond that, but I can see that there must be a simplification that doesn't require an analytic form for $f(n)$. – David G. Stork Dec 11 '20 at 06:00
  • This is a tough one. You can't assume that there are no factors in $(n, 2n)$. For example, taking $n = 30, ~45$ is a factor of $1800$. – user2661923 Dec 11 '20 at 06:24
  • Huh? But those factors do not enter the sum. – David G. Stork Dec 11 '20 at 06:26
  • Hmm, but I don't see how you get that the number of 2s is $\frac{10^{12}}{2}$ – Han Xiong Dec 11 '20 at 17:12
  • I wrote out F(10): 1+2+3+3+3+5+3+4+5+5, but it does not follow your method – Han Xiong Dec 11 '20 at 17:22
  • Ummm... $2$ is a factor or $2$, $4$, $6$, $8$, and $10$. There are $10/2 = 5$ such factors. So the number of factors of $2$ in $10^{12}$ is $10^{12}/2$. Right? – David G. Stork Dec 11 '20 at 18:10
  • Oh, yes, I think I misunderstood you, sorry. It is kind of like counting by 2's, right? – Han Xiong Dec 11 '20 at 18:40
  • The approach for calculating the sum wouldn't work. The number of $4$s isn't given by $\frac{10^{12}}{4}$, but would instead be $\frac{10^{12}}{2}$, since $2(2n)^2 \equiv 0 \pmod 4$. – Varun Vejalla Dec 11 '20 at 23:14