I want to compute the longest element $w_0$ of the Weyl group $W$ for $A_2$, $B_2$ and $G_2$. I saw this has already been asked before here for the case of $G_2$, but the answers are still not very clear to me. Indeed, I would like to prove this without using any notion about Coxeter groups and only using the properties of the longest element $w_0$: for instance, I know that $w_0$ is the unique element in $W$ such that $w_0$ sends all positive roots into negative ones and that $w_0^2 = id$. Finally, I know that every reduced expression of $w_0$ must contain all simple reflections (possibly appearing more than once). Any hints on how to proceed?
Asked
Active
Viewed 434 times
1
-
When you say "compute the longest element", what do you mean precisely? For instance, $G_2$ only has 12 elements anyway, $A_2$ has 6, and $B_2$ has 4. Surely any sufficiently explicit representation you'd care to name could then be brute-forced. Put another way, how does this question differ materially from "list all the elements of $A_2, B_2, G_2$"? – Joshua P. Swanson Dec 28 '20 at 14:43
-
I am interested in computing the longest element of the Weyl group, so the longest product of simple reflections in the Weyl group acting on each of the $A_2, B_2, G_2$, not the longest root in each of these. I hope I understood your question correctly. – cip Dec 28 '20 at 14:52
-
(Minor typo: $B_2$ has 8 element, not 4.) – Joshua P. Swanson Dec 29 '20 at 00:43
-
1Do you mean computing as a product of simple reflections? – Moishe Kohan Dec 29 '20 at 00:55
-
Yes, that’s what I mean. – cip Dec 29 '20 at 09:43
-
1For a general finite coxeter group, there is a nice formula via apower of coxeter element, see Knutson’s answer here: https://mathoverflow.net/questions/54926/longest-element-of-weyl-groups – Moishe Kohan Jan 01 '21 at 01:10
1 Answers
3
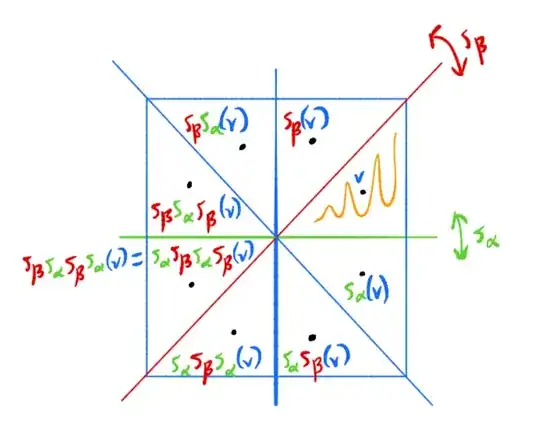
How are you describing the elements of these Weyl groups? Take $B_2$. I've drawn the standard picture below. I've picked a couple of simple reflections, $s_\alpha$ and $s_\beta$. They bound the fundamental Weyl chamber, which contains the point $v$. (Ok, I've added a square since I think of this group as symmetries of a square, but you can delete the square if you want.) I've applied the simple reflections $s_\alpha, s_\beta$ to $v$ in all possible ways, recording the shortest expression(s) for each point in the orbit. We can just read off that there is a unique longest expression, $s_\alpha s_\beta s_\alpha s_\beta(v) = s_\beta s_\alpha s_\beta s_\alpha(v)$. This is hence the longest element.
Joshua P. Swanson
- 9,634
-
1Thank you, this is exactly what I was looking for. I have a bunch of questions though: 1) why do the simple reflections $s_{\alpha}$ and $s_{\beta}$ bound the fundamental Weyl chamber? 2) Is it important to choose the fundamental chamber as a starting point? – cip Dec 29 '20 at 07:47
-
2
- The reflecting hyperplanes bound the fundamental Weyl chamber by definition. The root $\alpha$ is along the positive y-axis here since the fundamental chamber is above the green line, and likewise the root $\beta$ is pointing southeast. 2) It depends on what you mean. You can choose different simple roots and thereby make any chamber the fundamental one. The key fact is the Weyl group acts transitively and faithfully on the Weyl chambers, so the Weyl group is encoded in its action on the orbit of any point in such a chamber--that's what I drew.
– Joshua P. Swanson Dec 29 '20 at 11:12