5

For small values of $x$, the following widely used approximations follow immediately by Taylor expansion:

  1. $\sin x \approx x$
  2. $\cos x \approx 1-\frac{x^2}{2}$
  3. $\tan x \approx x +\frac{x^3}{3}$

I am looking for a justification of these approximations without the use of series expansions.

By purely geometric considerations, it is easy to see that for small values of $x$, we have

$$ \sin x < x < \tan x.$$

Division by $\cos x$ and an application of the squeeze lemma yield

$$\frac{\sin x}{x}\xrightarrow{x\to0}1$$

and hence the approximation (1.). Using the identity $\cos x = 1-2 \sin^2 \frac{x}{2}$, the approximation (2.) also follows.

Can one justify the approximation (3.) by a similarly elementary argument without using Taylor expansion?

I tried around using the angle addition theorems, but I did not really get anywhere, mainly because I could not make the factor $\frac13$ appear anywhere.

Mars Plastic
  • 4,239
  • 1
    This answer which is related to the analogous problem for sine might be insightful https://math.stackexchange.com/questions/2780550/evaluate-lim-x-to-0-fracx-sin-xx-sin-x-without-lhopital/2780697#2780697 – b00n heT Jan 01 '21 at 20:15
  • It's odd to hope to get a third-term Taylor polynomial without Taylor. I realize that there are lots of tricks, but I don't believe there is one here. Why are you even trying? – Ted Shifrin Jan 01 '21 at 20:29
  • @TedShifrin Well, it's also odd that you get a second term Taylor polynomial for the cosine function without using Taylor, isn't it? ;-) But yes, I'm aware that there is no particular reason for a simple solution to exist - I'm just hoping that someone knows a smart trick. – Mars Plastic Jan 01 '21 at 20:32
  • It's not odd for the cosine (pun noted) because that's the leading behavior of $1-\cos x$, and of course we all know a trig identity for $1-\cos x$. But if you write $\sin x - x$ you're out of the realm of trig. – Ted Shifrin Jan 01 '21 at 20:35
  • That's a valid point. Still, your advice combined with a third order Taylor expansion for the sine function (which can be proved purely by trigonometry, as hinted at by b00n heT) does in fact provide the kind of argument I am looking for for the tangent function. – Mars Plastic Jan 01 '21 at 20:39
  • Ah, I hadn't looked at that link. Yes, you're going to have to go that route and then do what I had immediately suggested. – Ted Shifrin Jan 01 '21 at 20:41
  • 1
    Well, you could maybe view those parts as the first few steps of the bootstrapping $\cos x = 1 + o(1) \rightarrow \sin x = \int_0^x \cos t,dt = x + o(x) \rightarrow \cos x = 1 - \int_0^x \sin t,dt = 1 - \frac{x^2}{2} + o(x^2)$. And then, next step would be $\sin x = \int_0^x \cos t,dt = x - \frac{x^3}{6} + o(x^3)$. – Daniel Schepler Jan 01 '21 at 20:54
  • A better second-order approximation of $\tan$ is $$ \tan(x) \approx x + \tfrac{3}{8} x^3$$ or $$ \tan(x) \approx \frac{x (x^2-8)}{4(x^2-2)}$$ – John Alexiou Jan 01 '21 at 20:58
  • Yes, it just occurred to me to do what @DanielSchepler just suggested. Without integrating, you can do this by a standard Mean Value Theorem argument. – Ted Shifrin Jan 01 '21 at 21:27
  • @JohnAlexiou I'm not sure what you mean by better approximation. The 3rd degree Taylor Polynomial is the unique polynomial with error $o(x^3)$. What are your errors? Your first statement certainly seems impossible to me. – Ted Shifrin Jan 01 '21 at 21:32
  • As already mentioned by @b00nhet this type of problem comes up a lot. I have posted a solution using tangents and bisection and another using sines and trisection so it certainly is feasible to get arbitrarily many terms of the Taylor series via trigonometry. – user5713492 Jan 01 '21 at 21:46
  • @TedShifrin - see the last part of my answer to see how my approximation is much closer to $\tan x$ than the one you mention. – John Alexiou Jan 01 '21 at 21:58

3 Answers3

6

Famously, a sector with a small angle proves $\lim_{x\to0}\tfrac{\sin x}{x}=1$ and hence$$\lim_{x\to0}\tfrac{1-\cos x}{x^2}=\lim_{x\to0}\tfrac{\sin^2\tfrac{x}{2}}{2(x/2)^2}=\tfrac12.$$We can improve the former result: if you approximate a sector's arc as a parabola, you can prove$$\lim_{x\to0}\frac{1-\tfrac{\sin x}{x}}{x^2}=\tfrac16.$$Finally,$$\lim_{x\to0}\frac{\tfrac{\tan x}{x}-1}{x^2}=\lim_{x\to0}\frac{\tfrac{\sin x}{x}-\cos x}{x^2}=\lim_{x\to0}\frac{1-\cos x}{x^2}-\lim_{x\to0}\frac{1-\tfrac{\sin x}{x}}{x^2}=\tfrac12-\tfrac16=\tfrac13.$$

J.G.
  • 115,835
0

Look at the trigonometric circle and approximate the chord $s$ with the angle $\theta$.

fig

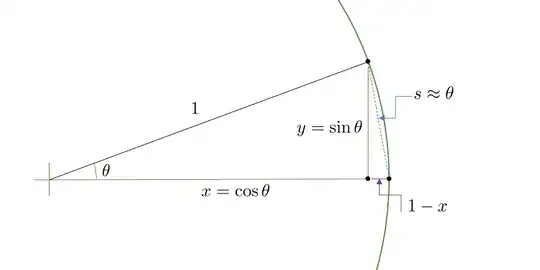
Here $x=\cos \theta$ and $y=\sin \theta$.

From the big triangle, you have $x^2+y^2=1$ which is obvious, and from the small circle, you have $s^2 = y^2 + (1-x)^2$. But with approximation $s \approx \theta$ the above is

$$\theta^2 \approx y^2 + (1-x)^2 \tag{1}$$

Now sub $y=\sqrt{1-x^2}$ to get the well-known approximation

$$ \theta^2 \approx 1-x^2 + (1-x)^2 = 2 (1-x) $$

or

$$ x = \cos \theta \approx 1 - \tfrac{1}{2} \theta^2 \tag{2}$$

Now use (2) in (1) to get $\theta^2 \approx y^2 + \tfrac{1}{4} \theta^4$, but since we are keeping this a second order approximation $\theta^4 \approx 0$ and

$$ y = \sin \theta \approx \theta \tag{3} $$

Finally, $\tan \theta = \tfrac{y}{x} \approx \tfrac{\theta}{1-\tfrac{1}{2} \theta^2}$. But use the property $\tfrac{1}{1-z} = 1 + \frac{1}{1-z} z \approx 1 + z$ with $z=\tfrac{1}{2} \theta^2$ to get the final approximation.

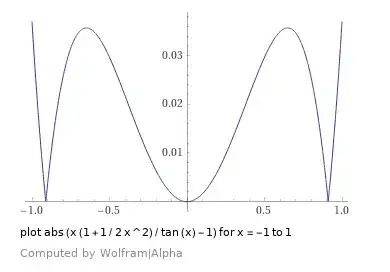
$$ \tfrac{y}{x} = \tan \theta \approx \theta \left( 1 + \tfrac{1}{2} \theta^2 \right) \tag{4a} $$

But note that the last one is based on two approximations.

Another approach with $\tan$ would be to approximate once $\tan \theta = \tfrac{y}{x} = \theta \frac{\sqrt{1-\tfrac{1}{2}z}}{1-z}$ with $z=\tfrac{1}{2}\theta^2$ and the approximation $ \tan \theta \approx \theta \left( 1 + \tfrac{3}{4} z \right)$

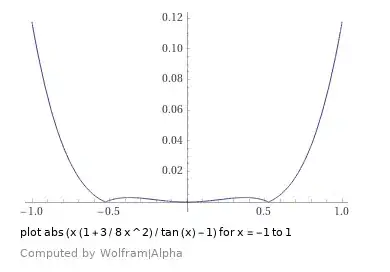
$$ \tfrac{y}{x} = \tan \theta \approx \theta \left( 1 + \tfrac{3}{8} \theta^2 \right) \tag{4b} $$

For example with $\theta=0.6$ you have $\tan(0.6) = 0.68413681$, $0.6 \left( 1 + \tfrac{1}{2} 0.6^2 \right)=0.708$ an 3.5% error, and $0.6 \left( 1 + \tfrac{3}{8} 0.6^2 \right)=0.681$ an 0.45% error.

So (4b) is at least an order of magnitude better at approximating $\tan \theta$ than (4a). A graphical comparison of the error $f(x)/\tan x-1$ is shown below:

fig2 fig3

John Alexiou
  • 13,816
  • I do not accept your claim that this is a better approximation unless you give me a rigorous bound. If you're measuring error a different way to justify the claim, please make it explicit. I don't see your justifying that the error is small compared to the (unique) Taylor polynomial. And one example is no proof. – Ted Shifrin Jan 01 '21 at 22:05
  • Ok, look at the graphs of the error and see why I assert an order of magnitude improvement. – John Alexiou Jan 01 '21 at 22:08
  • Two complaints: You are not using the Taylor polynomial for a comparison. OK, so you're looking at relative error. My claim should still hold if you do Taylor. – Ted Shifrin Jan 01 '21 at 22:14
  • I am comparing a function $f(x)$ to tangent by computing the relative error $$\text{error} = \frac{| f(x) - \tan x |}{|\tan x |} =\left| \frac{f(x)}{\tan x}-1 \right|$$ how is it wrong? – John Alexiou Jan 01 '21 at 22:15
  • Sorry. I misread your code at first. Taylor polynomial relative error still is optimal. Better check your reasoning. It's easy to prove that if the Taylor Polynomial has optimal error (unique polynomial with error $o(x^3)$, then the relative error will be optimal (uniquely with size $o(x^2)$ in this case). – Ted Shifrin Jan 01 '21 at 22:16
  • How is a 3.5% error better than a 0.45% error for the sample value of $x=0.6$. If you want try different smaller angles and compare the two yourself. here is a plot of the error in the same graph. – John Alexiou Jan 01 '21 at 22:20
  • You refuse to consider the Taylor polynomial. I'm done with this discussion. – Ted Shifrin Jan 01 '21 at 22:22
  • Taylor polynomial is optimal for $x=0$, but there are other ways to approximate functions that are optimal across a wider range. The Taylor polynomial of what order are you referring to? I am considering the baseline to be $\tan(x)$ which equals to the Taylor with infinite terms. – John Alexiou Jan 01 '21 at 22:23
  • I've asked you repeatedly to make a mathematical statement of what "error" means. Your computations are based on $x\approx 0$. And you refuse to make a rigorous definition. You are not using $L^2$ or any other notion that I can see. And, for the fourth time, you have not compared your two approximations with the Taylor polynomial. – Ted Shifrin Jan 01 '21 at 22:25
0

Proof that $\boldsymbol{\lim\limits_{x\to0}\frac{x-\sin(x)}{x^3}}=\frac16$

As shown in $(2)$ from this answer, since $\cos(x)$ is continuous, given any $\epsilon\gt0$, we can find a $\delta\gt0$ so that if $0\lt|x|\le\delta$, we have $$ 1-\epsilon\le\cos(x)\le\frac{\sin(x)}x\le1\tag1 $$ Thus, assuming $0\lt|x|\le\delta$, $$ \begin{align} \frac{x-\sin(x)}{x^3} &=\frac1{x^3}\sum_{n=0}^\infty\left(2^{n+1}\sin\left(x/2^{n+1}\right)-2^n\sin\left(x/2^n\right)\right)\tag{2a}\\ &=\frac1{x^3}\sum_{n=0}^\infty\left(2^{n+1}\sin\left(x/2^{n+1}\right)-2^{n+1}\sin\left(x/2^{n+1}\right)\cos\left(x/2^{n+1}\right)\right)\tag{2b}\\ &=\frac1{x^3}\sum_{n=0}^\infty2^{n+1}\sin\left(x/2^{n+1}\right)\left(1-\cos\left(x/2^{n+1}\right)\right)\tag{2c}\\ &=\frac1{x^3}\sum_{n=0}^\infty\frac{2^{n+1}\sin^3\left(x/2^{n+1}\right)}{1+\cos\left(x/2^{n+1}\right)}\tag{2d}\\ &=\frac12\sum_{n=0}^\infty\frac1{2^{2n+2}}\left[(1-\epsilon)^3,\frac1{1-\epsilon/2}\right]\tag{2e}\\ &=\frac16\left[(1-\epsilon)^3,\frac1{1-\epsilon/2}\right]\tag{2f} \end{align} $$ Explanation:
$\text{(2a)}$: apply $\lim\limits_{x\to0}\frac{\sin(x)}x=1$ and the telescoping sum
$\text{(2b)}$: $\sin(2x)=2\sin(x)\cos(x)$
$\text{(2c)}$: factor
$\text{(2d)}$: $\sin^2(x)=(1-\cos(x))(1+\cos(x))$
$\text{(2e)}$: apply $(1)$ with $[a,b]$ representing a number in that range
$\text{(2f)}$: evaluate the sum

Therefore, by $(2)$ and the Squeeze Theorem, $$ \lim_{x\to0}\frac{x-\sin(x)}{x^3}=\frac16\tag3 $$

The Approximations

The limit $(3)$ gives the following approximation $$ \sin(x)\approx x-\frac{x^3}6\tag4 $$ Since the Binomial Theorem gives $(1-x)^2=1-2x+x^2\approx1-2x$, we have $\sqrt{1-x}\approx1-\frac x2$. $$ \begin{align} \cos(x) &=\sqrt{1-\sin^2(x)}\tag{5a}\\ &\approx\sqrt{1-x^2}\tag{5b}\\ &\approx1-\frac{x^2}2\tag{5c} \end{align} $$ Finally, since the Geometric Series gives $\frac1{1-x}=1+x+x^2+\dots\approx1+x$, $$ \begin{align} \tan(x) &=\frac{\sin(x)}{\cos(x)}\tag{6a}\\ &\approx\left(x-\frac{x^3}6\right)\left(1+\frac{x^2}2\right)\tag{6b}\\ &\approx x+\frac{x^3}3\tag{6c} \end{align} $$

robjohn
  • 345,667