$\pi$ & $\phi$ (Golden ratio), Pentagon inscribed in unit circle

Question

Everyone is aware that square inscribed in unit circle and infinite product giving rise to $\pi$. One of the simplest way to represent $\pi$ with the help of nested radical as follows $$\pi = \lim_{n\to \infty} 2^n\cdot \sqrt{2-{\sqrt{2+\sqrt{2+\sqrt{2+...}}}}}\tag1$$

where number of 2 inside the nested radicals is n. Viete's formula for $pi$

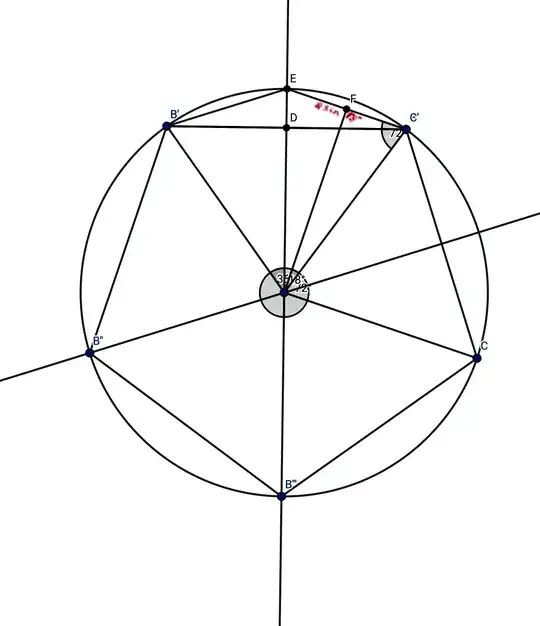
Approach to get similar result with inscribed initial polygon as PENTAGON will be as follows..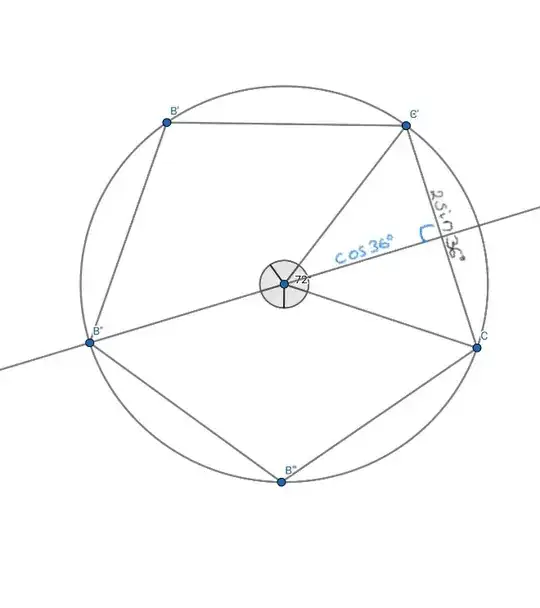

According to Chord in Trigonometry

1. A perpendicular line from the centre of a circle bisects the chord. Or otherwise can be stated as, 2. The line segment through the centre bisecting a chord is perpendicular to the chord.

The length of the chord inside the unit circle for Pentagon will be $2\sin36^\circ$. Therefore circumference of Regular pentagon will be $5\times2\sin36^\circ$.

For the sake of simplicity let us apply rules which are basic

$$2\sin\frac{\pi}{5} = \sqrt{2 - 2\cos\frac{2\pi}{5}}$$

Now doubling the sides the length of the each chord inside the unit circle will be $2\sin(\frac{\pi}{2\cdot5})$ and therefore circumference of decagon is $5\cdot2^2\sin18^\circ$. where $2\sin18^\circ = \sqrt{2-2\cos\frac{\pi}{5}}$

Therefore circumference can be represented as $C_{10} = 5\cdot2^1\sqrt{2-2\cos\frac{\pi}{5}} = 5\cdot2^1\sqrt{2-\phi}$

(Here we get $2\cos\frac{\pi}{5} = \phi $, the Golden ratio)

As $\pi = \frac{C}{D}$

Iterating the sequence we get the circumference of infinitely increasing polygons as follows and simplifying for $\pi$

Assuming doubling from Pentagon as initial polygon

For Pentagon, calculating $\pi$ as $\frac{C}{D}$

Circumference of Pentagon is $5\times 2\sin\frac{\pi}{5} = 5\cdot\sqrt{2-2\cos\frac{2\pi}{5}}$ (by Half angle cosine formula). As the diameter is 2 in unit circle. Value of $\pi_{n}$ where n represents the number of sides of the polygon of increasing order, i.e. doubling everytime from Pentagon

From Regular Pentagon $\pi_{5}$ = $\frac{1}{2}\cdot 5\cdot\sqrt{2-2\cos\frac{2\pi}{5}} = \frac{5}{2}\cdot\sqrt{3-\phi} = 2.938926...$

From decagon $\pi_{5\cdot2^1} = 5\cdot2\sin\frac{\pi}{5\cdot2} = 5\cdot\sqrt{2-2\cos\frac{\pi}{5}} = 5\cdot\sqrt{2-\phi} = 3.0901699...$

From icosagon (20 sided polygon) $\pi_{5\cdot2^2} = 5\cdot2^2\sin\frac{\pi}{5\cdot2^2} = 5\cdot2^1\cdot\sqrt{2-2\cos\frac{\pi}{5\cdot2^1}} = 5\cdot2^1\cdot\sqrt{2-\sqrt{2+2\cos\frac{\pi}{5}}} = 5\cdot2^1\sqrt{2-\sqrt{2+\phi}} = 3.128689...$

From 40gon

$\pi_{5\cdot2^3} = 5\cdot2^2\sqrt{2-\sqrt{2+\sqrt{2+\phi}}} = 3.138363...$

From 80gon

$\pi_{5\cdot2^4} = 5\cdot2^3\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\phi}}}} = 3.140785...$

And so on

The value of $\pi$ for $5\cdot2^{10}$gon is $\pi_{5\cdot2^{10}}=3.14159245...$

$$\pi = \lim_{n \to \infty} 5\cdot2^n\sqrt{2-\sqrt{2+\sqrt{2+...\text{(n terms)}+\phi}}} \tag2$$ by applying limits $2^n$ becomes infinitely large and nested radical becomes infinitely small. The resulting value of $\pi$ is increasingly accurate and converges little faster compared to $\pi$ from incribed polygon as square.

The question is

$Equation1 \over Equation2$ $= 5$ explained as follows

$\frac{\pi}{\frac{\pi}{5}} = 5 = \frac{\lim_{n\to\infty}2^n\cdot\sqrt{2-\sqrt{2+\sqrt{2+...\text{n times}}}}}{\lim_{n\to\infty}2^n\cdot\sqrt{2-\sqrt{2+\sqrt{2+...\text{n times}+\phi}}}}$ (The $2^n$ gets cancelled out)

How to explain the fact that $\sqrt{2-\sqrt{2+\sqrt{2+...+\phi}}}$ is an infinitely small number different from $\sqrt{2-\sqrt{2+\sqrt{2+...+\sqrt{2}}}}$ another infinitely small number which is 5 times larger than the the first one? (By the geometric method we are deriving the value of $\pi$ from right side proceeding towards left to get the value of nested square root. (Computing also does the same). It seems that we should change the conventional thinking of representing infinite nested radicals in this respect. I need comments on this)

Infinite expansion happens between both ends. Can we call these as INFINITELY EXPANDING BALLOON NESTED RADICALS? 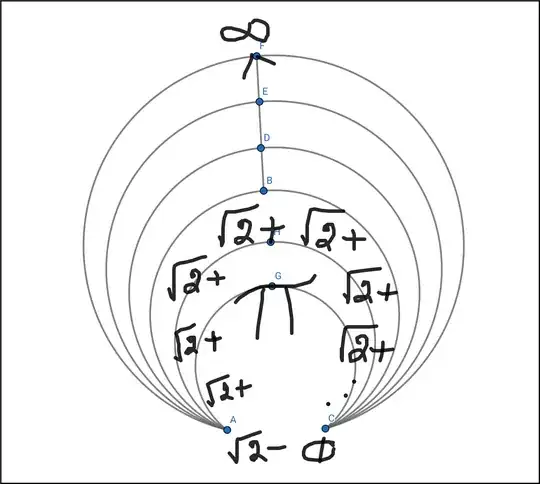(Bear with me for poor image quality)

When trigonometry is more concerned with unit circle practically, is $\epsilon = \frac{\pi}{\infty}$(all operations as in real number systems, here also it is applicable) different from traditional $\epsilon = \frac{1}{\infty}$? (Even though it looks trivial) (Of course there are different ways to get the infinitesimals in surreal/hyperreal number systems)

By deriving $\pi$ from polygons other than square, equilateral triangle and pentagon, probably it may be possible to get infinite number of infinitesimals by the way of representing as nested square roots. Please comment or clarify on these.

Answer 1

George Orwell would say that all infinitely small numbers are small, but some of them are more small than others.

An infinitely small number $\varepsilon$ is an informal understanding of a sequence $(\varepsilon_n)$ of real numbers converging to zero, as your nested radicals. The smallness of $\varepsilon$ can be thought as a convergence speed of $(\varepsilon_n)$. This understanding provides a huge hierarchy of infinitely small numbers.

For each infinitely small number $\varepsilon=(\varepsilon_n)$ which is non eventually zero and each positive real $\lambda$, a sequence $(\lambda\varepsilon_n)$ converges “in $\lambda$-times” slower, and can be thought as an infinitely small number $\lambda\varepsilon$. So, for instance $\tfrac 12\varepsilon$ is smaller than $\varepsilon$. But an infinitely small number can be even smaller than $\lambda\varepsilon$ for each $\lambda>0$. For instance, a sequence $(\varepsilon^2_n)$ eventually converges quicker than $(\lambda \varepsilon_n)$.

I guess that in a non-standard analysis infinitely small numbers are explicitly provided in an extension of a field of real numbers. So we can add and multiply them, but when we divide by an infinitely small numbers then as a result we can obtain an infinitely large number.

PS. Let $\mathcal P$ be a set of infinitely small numbers $(\varepsilon_n)$, such that all members $\varepsilon_n$ are positive. We can endow $\mathcal P$ with a preorder $\le$, putting $(\varepsilon_n)\le (\delta_n)$, if $(\varepsilon_n)\le (\delta_n)$ for all sufficiently large $n$. It turns out that this preorder has interesting set-theoretical properties.

For any sequence $(\varepsilon_n)_1, (\varepsilon_n)_2,\dots$ of elements of $\mathcal P$ there exists $\delta=(\delta_n)\in\mathcal P$ such that $\delta\le (\varepsilon_n)_i$ for each $i$. Indeed, it suffices to put $\delta_n=\min_{i\le n} (\varepsilon_n)_i$ for each $n$. Moreover, we can define $\mathfrak b$ be the smallest cardinality of a subset $B$ of $\mathcal P$ such that there exists no $\delta\in \mathcal P$ such that $\delta\le\varepsilon$ for each $\varepsilon\in B$ and $\mathfrak d$ be the smallest cardinality of a subset $D$ of $\mathcal P$ such that for each $\varepsilon\in \mathcal P$ there exists no $\delta\in D$ such that $\delta\le\varepsilon$. Clearly, $\omega_1\le \frak b\le\frak d\le \frak c$. It turns out, that values of $\frak b$ and $\frak d$ depend on additional axiomatic assumptions. For instance, Continuum Hypothesis implies $\omega_1=\frak b=\frak d=\frak c$, but each of claims $\omega_1=\frak b<\frak c$, $\omega_1=\frak d<\frak c$, $\omega_1<\frak b<\frak c$, $\omega_1<\frak d<\frak c$, $\omega_1<\frak b=\frak c$, and $\omega_1<\frak d=\frak c$ is consistent with ZFC, see, for instance, Section 5 of [vDou].

References

[vDou] Eric K van Douwen, The integers and Topology, in: K.Kunen, J.E.Vaughan (eds.) Handbook of Set-theoretic Topology, Elsevier, 1984, 111–167.

Answer 2

This has nothing to do with nested radicals.

Let the sequence $a_n$ be $1,1/2,1/3,1/4,1/5,1/6,1/7,\dots$.

Let the sequence $b_n$ be $1/5,1/10,1/15,1/20,1/25,1/30,1/35,\dots$.

Then $a_n/b_n$ is the sequence $5,5,5,5,5,5,5\dots$.

So $\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=0$, but $\lim_{n\to\infty}(a_n/b_n)=5$.

What's the problem?