$u_t+(u(1-u))_x=a(1-2u)$, transients to steady solution

Question

We consider the non conserving equation $$u_t+(f(u))_x=af'(u)$$ where $a$ is a constant, 0$\leq$ x $\leq$ 1 and $f(u)=u(1-u)$.

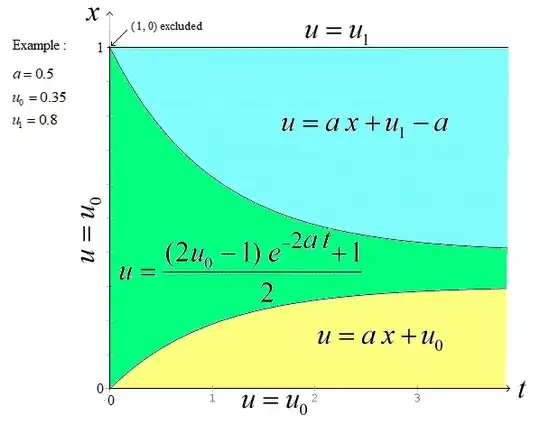
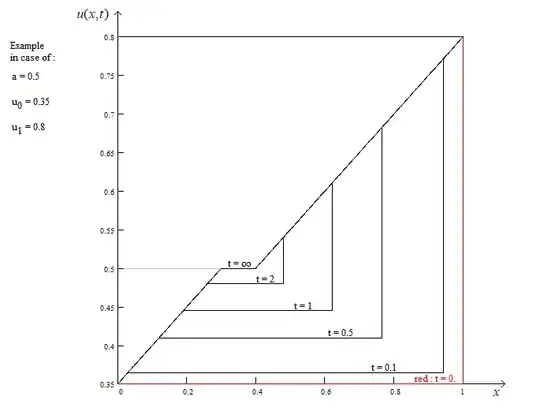
The steady solution of this equation with boundary condition $u(0)=u_0$ and $u(1)=u_1$ can be obtained by putting $u_t=0$ and the solution obtained are $u=1/2, u=ax+u_0$ and $u=ax+u_1$

I am trying to solve this equation by method of characteristics to obtain the transient solution with the some given initial condition u(x,0).

By method of characteristics, I have $\displaystyle \frac{dt}{1}=\frac{dx}{1-2u}=\frac{du}{a(1-2u)}$, this means that the characteristics equation is $$\displaystyle \frac{dx}{dt}=1-2u$$ along with $\displaystyle \frac{du}{dx}=a, \displaystyle \frac{du}{dt}=a (1-2u).$

Solving these equations, I reached upto $u(x,t)=\displaystyle\frac{1-(1-2u_0)e^{-2at}}{2}$.

As I am trying to reach to the steady solution, I must apply $t \rightarrow \infty$ which gives me $u=1/2$.

But I also have another solution $u=ax+u_0$ which is obtained at a steady state.

Does changing the initial condition in some way can help me reach the other solution or I am not solving this equation in a correct way. I have also tried to solve this equation using the Reimann condition this post still, I reach the solution $u=1/2$ on applying $t\rightarrow \infty$. Thanks in advance for any help.

Answer 1

$$u_t+(1-2u)u_x=a(1-2u).$$ You correctly wrote the Charpit-Lagrange system of ODEs : $$\frac{dt}{1}=\frac{dx}{1-2u}=\frac{du}{a(1-2u)}.$$ A first characteristic equation comes from solving $\quad \frac{dx}{1-2u}=\frac{du}{a(1-2u)}$ $$u-ax=c_1$$ A second characteristic equation comes from solving $\quad \frac{dt}{1}=\frac{du}{a(1-2u)}$ $$(2u-1)e^{2at}=c_2$$ The general solution expressed on the form of implicit equation $c_2=F(c_1)$ is : $$(2u-1)e^{2at}=F(u-ax)$$ Or alternatively $$u-ax=G\big((2u-1)e^{2at}\big)$$ $F$ or $G$ are arbitrary functions, one inverse of the other. They are to be determined according to some condition.

IN ADDITION :

After the clarification of the boundary and initial conditions (In comments).

The specified conditions are $\quad\begin{cases} u(0,t)=u_0 \neq \frac12\\ u(1,t)=u_1 \neq \frac12\\ u(x,0)=u_0 \neq u_1 \end{cases}$

There is not much calculus to do to observe that there is no solution if $F$ or $G$ are continuous functions.

We have to consider piecewise functions. To some extend this is similar to the Burger's PDE where there is a transition frontier namely "shock". This might be not the right term in the present case but doesn't mater the denomination.

With piecewise functions they are a lot of different cases depending on the values of $u_0,u_1,a$. For exemple the schematic below gives a rough idea of the behaviour.

Along the border $x=0$ we have $U_t=0$. This is the case of constant above function $G$.

Along the border $x=1$ we have $U_t=0$. Again the function $G$ is constant, but different.

Along the border $t=0$ we have $U_x=0$. This is the case of constant above function $F$. In other words : $u(x,0)=u_0\quad\implies\quad (2u_0-1)=F(u_0-ax)$. This is possible only if $F$ is a constant function : $F=2u_0-1$. Thus $\quad (2u-1)e^{2at}=2u_0-1$ and the solution is : $$u=\frac{(2u_0-1)e^{-2at}+1}{2}.$$

On the transition line which separates the fields green and blue on the figure, the function $u(x,t)$ is discontinuous. The values of $u$ are not equal on both sides of the line.

Below another presentation of the same example shows what happens for $t\to\infty$ in this case. The shapes can be different for other values of $a,u_0,u_1$.

Note that the above figures are not to intend to explain all cases. More work would be necessary for different cases depending on the values of $u_0,u_1,a$.

Answer 2

Consider the initial-value problem $u(x,0) = U^0(x)$ with $U^0(x) = ax+C$. This problem amounts to setting $v=1-2 u$ initially equal to $f(x) = 1-2 U^0(x)$, using the notations of my previous answer. The solution deduced from the method of characteristics therein leads to $$ v(x,t) = 1-2 U^0(x) , \qquad u(x,t) = U^0(x) , $$ showing that $u = U^0(x)$ is a steady state (i.e., the solution of the corresponding initial-value problem does not depend on time). Taking the limit $t\to \infty$ still provides $u \to U^0(x)$.

Now, consider the initial conditions $u(x,0) = U^\text{0}(x) + \epsilon U^{1}(x)$ where $\epsilon$ is a small perturbation. The method of characteristics yields the implicit equation $$ v^1 = -2U^1\!\left(x-(v^0 + \epsilon v^1)\frac{e^{2at}-1}{2a}\right) , $$ where we have inserted the Ansatz $v(x,t) = v^0(x) + \epsilon v^1(x,t)$ with $v^0(x) =1-2U^0(x)$. At leading order in $\epsilon$, we find $$ v^1 = -2U^1\!\left(xe^{2at} + (2C-1)\frac{e^{2at}-1}{2a}\right) . $$ Thus, if the perturbation $U^1(x)$ is vanishing fast enough at $x\to\pm\infty$, then the IVP's solution might still tend towards the steady state $U^0(x)$ as $t\to \infty$.