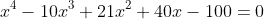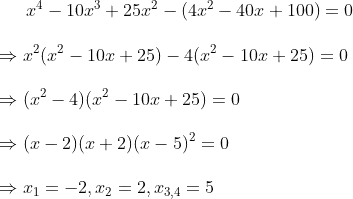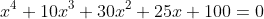A user named 'Uzdawi' from another post asked a question about how to solve the quartic function of
One of the responses included an answer from the user 'Peđa Terzić', which is as follows:
Could anyone kindly elaborate on the method used to get to the answer please.
And how the same method could be used to solve the following function:
If not the same method used by Peđa Terzić, how else could you approach to solving a quartic function?
Thank you for your time.
In a case like this, I would pretend I was a high-school student and use the Rational Root Theorem, which says, here, that the only rational roots (if any) will be from the set $\{\pm1,\pm2,\pm4,\pm5,\pm10,\pm20,\pm25,\pm50,\pm100\}$.
Starting systematically, you see that $\pm1$ aren’t roots, but $+2$ is. Then divide by $x-2$ to try to find the roots of $x^3-8x^2+5x+50$.
The RRT tells you to check $\{\pm1,\pm2,\pm5,\pm10,\pm25,\pm50\}$, and you already know that $\pm1$ are no good. Trying $+2$ is no good, but you try $-2$ and see that that’s a root too. And the quotient $(x^3-8x^2+5x+50)/(x+2)$ is $x^2-10x+25=(x-5)^2$, so that you’re done.
No ingenuity.
(In this very special case)
EDIT (addendum):
I notice that I originally omitted the possibilities $\pm20$ from the original list. I have included them now, but I might as well take the opportunity to adduce additional information:
If you know the magic of the Newton Polygon, you see that if you draw the two diagrams for the primes $2$ and $5$ and the original polynomial, both have their only vertices at $(0,2)$, $(2,0)$, and $(4,0)$. The only slopes are $-1$ and $0$. This means that a root can be only singly divisible by $2$ or $5$. In other words, the only possibilities are from $\{\pm1,\pm2,\pm5,\pm10\}$. You’d still need to do the computational work I did above, though.
What he did there from the first equation to the second was a very convenient rearrangement of the expression, in such a way that the quartic polynomial became factorable. For example, note that he wrote $21x^2$ as $25x^2$ followed by adding a $-4x^2$.
The real "magic" happened from $$ x^4-10x^3+21x^2+40x-100=0. \tag{1} $$ to $$ x^4-10x^3+25x^2-(4x^2-40x+100)=0. \tag{2} $$ The rest of the solution consists of high school algebraic manipulations.After written in terms of factors, it's easy to get the roots.
There is no algorithmic method for doing what he did from (1) to (2). It takes mathematical maturity and some ingenuity. Another way to solve a quartic equation is numerically, because not all quartic equation will factor out nicely like that.
The approach you described is based on clever factorization of the quartic into the product of two quadratics. A process for doing that is described here.
Another approach is to use the formulas for solving quartics. See here.
If you want to write software to solve quartics, ask again, because there are some nasty numerical problems that you'll need to deal with.
