In a paper I found a description of subsets of the Mandelbrot set called veins (these are also described in earlier papers by other authors, for example Chapters 20-22 of the Orsay Notes by Adrien Douady and John H. Hubbard):
Given a dyadic number $θ ∈ S^1=\mathbb{R}/\mathbb{Z}$, we define its complexity as $‖θ‖:= \min\left\{k≥0:D^k(θ) = 0 \mod 1\right\}$. Of course, if $θ = p/2^q$ with $p$ odd, then $‖θ‖=q$. Given an interval $(θ_−,θ_+)$ with $θ_−< θ_+$, we define its pseudocenter $θ_0$ to be the dyadic rational of lowest complexity inside the interval $(θ_−,θ_+)$. A pair of elements $(θ_−,θ_+)$ is a ray pair if the two external rays of angle $θ_−$ and $θ_+$ combinatorially land at the same parameter on the boundary of the Mandelbrot set.
Definition 6 Given a dyadic rational number $θ_0$, we define the combinatorial vein of $θ_0$ as the set of ray pairs $(θ_1,θ_2)$ such that:
$θ_0$ is the pseudocenter of $(θ_1,θ_2)$;
$N(θ_0) = N(θ_1)$.
-- Generalizations of Douady's magic formula Adam Epstein, Giulio Tiozzo https://arxiv.org/abs/1911.03796
Here $D(\theta)$ is the angle doubling map and $N(\theta)$ counts the number of ends of the Hubbard tree for $\theta$.
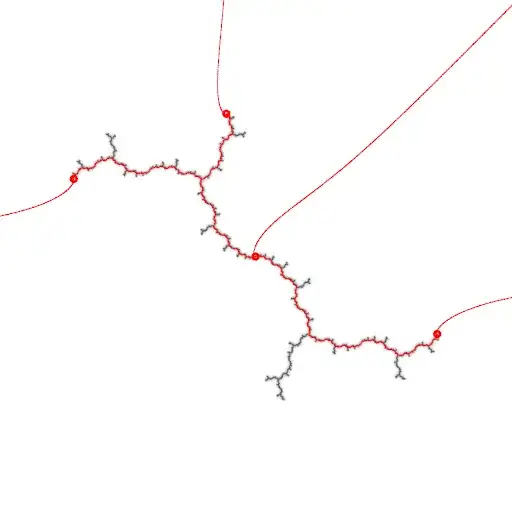
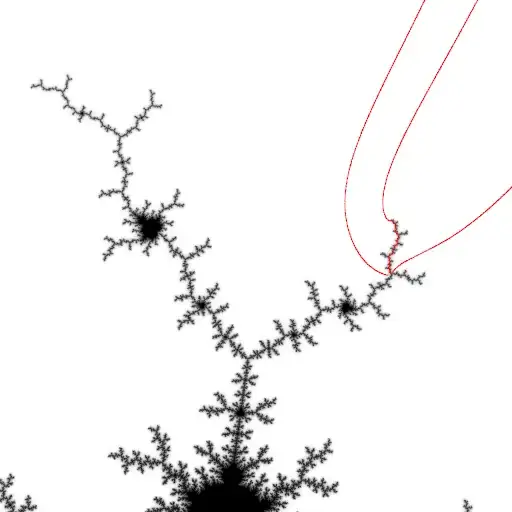
I can draw Hubbard trees implicitly given preperiodic rational $\theta$ (the Julia sets are dendrites, and neighbourhoods of pixels whose dynamic angles surround a ray landing on one of the marked points (preperiodic critical orbit) of the Hubbard tree are included into the drawn tree).
But if I apply this algorithm naively to the Mandelbrot set in an attempt to draw the vein from $\theta_0$, I will miss the second condition and extend the vein too far (the paper has some examples).
Counting the ends of a Hubbard is presumably possible using symbolics of pairs of dynamic rays landing on marked points, but this requires knowing the external angle and I have an arbitrary $c$ in the Mandelbrot set. I could trace the external parameter rays landing near $c$ to find angles, and if I knew the ray pair at the origin of the vein (the widest ray pair satisfying the conditions) I could use this to prune the results of the naive algorithm (mark the pixel only if both in the extended wrong "vein" and the angle is inside this interval).
So (at least) two methods for solving the problem, but maybe there's a still-better alternative?
Question: determine the ray pair at the origin of a vein given $\theta_0$.