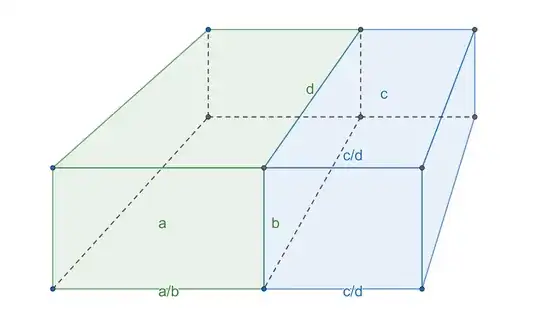
I've found visualizations of simple mathematical concepts to be a really useful tool in building intuition for more complex mathematical concepts. For example, this visualization of $(a + b)(c + d) = ac + ad + bc + bd$ can be used to visualize the calculus product rule.
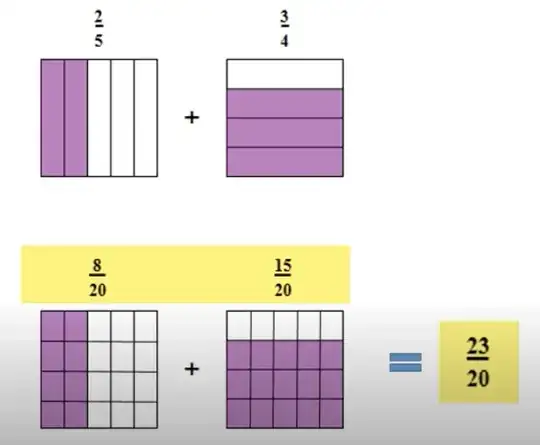
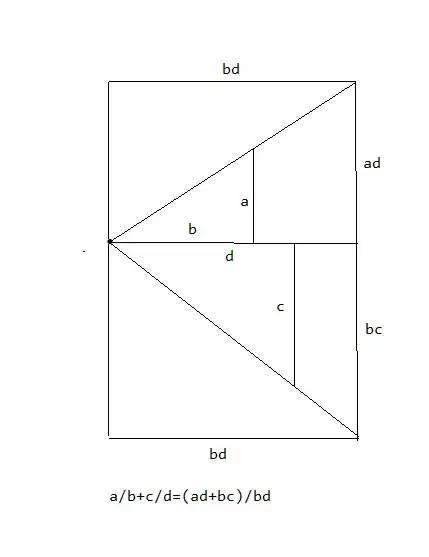
That being said, does anyone know of a visual way to show the following equation? $$ \frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd} $$