1

So I had this school assignment with this question

$\int (\cos x - \sin x)^2 \ dx$

And through computations I came up with this:

$\int (\cos x + \sin x )\ dx - \int 2 \cos x \sin x$

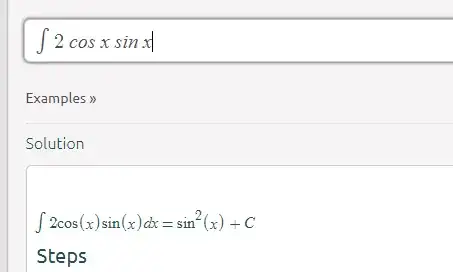
And this is where I got stuck, that when I integrate $2 \cos x \sin x$ right away, I would actually get $\color{blue}{x - \sin^2 x + C}$, which is different if I applied the double angle trigonometric identities in $2 \cos x \sin x$ , rewrite it to $\sin 2x$ , and it will give me a different answer, $\color{red}{x + \cos(2x)/2 + C}$

I went to Symbolab, and it really shows the difference, whether I integrate it right away or apply the trigonometric identity first before integrating

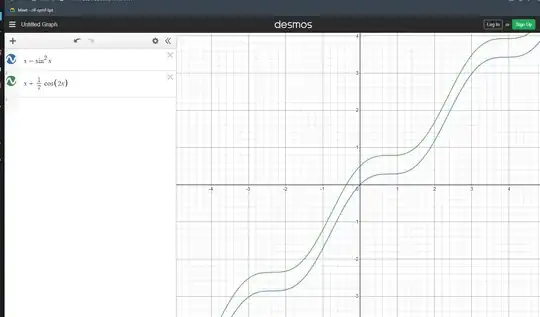
enter image description here

enter image description here

I tried to plot the points in Desmos, two answers seems close enough that it's just one constant away (particularly $0.5$), but still mathematically not equal.

enter image description here

So, does this mean that this trigonometric identity changed the actual answer that I should avoid using it as much as possible. Or this is just an exception? Which one is right? Is it both of the two answers?

I already passed my answer to the teacher, but what I actually did before passing it is integrating right away. But this problem haunts me in sleep that I actually opened my pc to ask this question here. Still learning integration techniques that I got introduced to this kind of problem, that overall it's pretty fun and stressing.

Rohit Singh
  • 1,143
Omeleto
  • 23
  • 5

5 Answers5

3

The "part of the antiderivative without the $+C$" is not unique, it can always be adjusted by a constant. Confusingly, there are expressions that don't appear to involve constants that nevertheless differ by constants, such as $\cos(x)^2$ and $-\sin(x)^2$. This is what is happening here:

$$\int 2 \sin(x) \cos(x) dx = \sin(x)^2 + C \\ \int \sin(2x) dx = -\frac{1}{2} \cos(2x) + C = -\frac{1}{2} \cos(x)^2 + \frac{1}{2} \sin(x)^2 + C = -\frac{1}{2} + \sin(x)^2 + C$$

where in that last step I used $\cos(x)^2=1-\sin(x)^2$.

These have to be the same thing, because the functions being integrated are the same...and they are the same thing, because $-1/2 + C$ in the second version is just another arbitrary constant. I find this is intuitive after you've "isolated" the constant like I did above, whereas the idea that $\sin(x)^2+C$ and $-\frac{1}{2} \cos(2x) + C$ are the same thing is a bit puzzling on its face.

Ian
  • 101,645
2

Hint:

$$x-\sin^2(x)+\color{blue}C=x+\frac{\cos(2x)}2+\color{blue}{C- \frac12}$$

Maximilian Janisch
  • 13,536
  • 1
    But the left part didn't equate to the case when I applied the trig identity first before integrating. It doesn't have 1/2 on it, or is that the same? – Omeleto Feb 10 '21 at 16:10
1

Depending on when and what you do the u-substitution, there are at least three ways to calculate $\int 2\sin(x)\cos(x)dx$:

$$ \int 2\sin x\cos x\ dx=\int \sin(2x)\ dx=-\frac12 \cos(2x)+C\tag{1} $$

$$ \int 2\sin x\cos x\ dx = (\sin x)^2+C\tag{2} $$

$$ \int 2\sin x\cos x\ dx = -(\cos x)^2+C\tag{3} $$

These answers are all correct.

In general, if you get (correctly via different methods) $$ \int f(x)\ dx=F(x)+C,\quad \int f(x)\ dx=G(x)+C $$

then there is some constant $K$ such that $G(x)=F(x)+K$.

Recall that $\int f(x)\,dx=F(x)+C$ really means $F'(x)=f(x)$ (on some interval $I$). The solution $F$ is not unique.

To see another example, both the following are correct: $$ \int \cos(x)\,dx=\sin x+C,\quad \int \cos(x)\,dx=\sin x+1+C $$

1

A common mistake.

$$\int(2\sin x\cos x-\sin 2x)\,dx=C,$$ so

$$\int2\sin x\cos x\,dx=\int\sin 2x\,dx+C$$ for some $C$.

-1

I=∫2cosx sinx dx=2∫cosx sinx dx .....1)
integration by parts
I=2{cosx∫sinx dx-∫ [d/dx(cosx)]* [ ∫sinx dx ] }dx
I=2{cosx (-cosx)- ∫ [-sinx][-cosx)]dx }
I=-2cos²x - 2∫[sinx][cosx]dx
from.....1)
I=-2cos²x -I
2I=-2cos²x
I=-cos²x + constant
I=-(1+cos2x)/2 + constant
I=-1/2-cos2x/2 + constant
I=-cos2x/2 + constant-1/2........(-1/2 is also constant) I=-cos2x/2 +C
∫sin2x dx= -cos2x/2 +C

Shreedhar Lohar
  • 7
  • 1