4

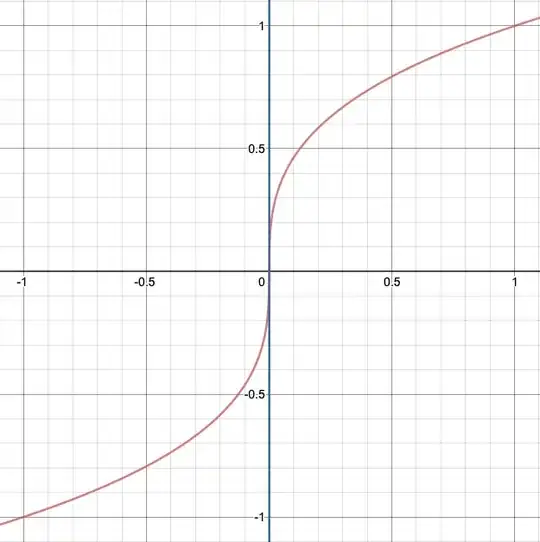
The graph of the function $f:x \mapsto x^{1/3}$ has a 'vertical tangent' at $x=0$:

Vertical tangent

Although this idea is certainly geometrically sound, from what I understand the tangent line is defined by the derivative, not vice versa. In other words, the tangent line to a function at the point $(a,f(a))$ is simply the line given by the equation $$ y - f(a) = f'(a)(x-a) \, , $$ where $f'(a)$ is of course defined as a limit. Since $f'(0)$ does not exist in this case, I'm unsure if we can truly say that the graph has a vertical tangent. The intuitive idea of a tangent 'just touching' the curve breaks down when we consider, for instance, the graph of a linear function, where the tangent touches the graph of the function itself at infinitely many points. Nevertheless, I have heard people say that the tangent line is fundamentally a geometric concept. Although the slope of the tangent line 'agrees' with the derivative if the derivative exists, there are instances where the tangent line is a meaningful concept even when the derivative doesn't exist. If this be the case, then what is the formal definition of a tangent?

Joe
  • 19,636
  • 2
    Vertical lines having undefined slope is a consequence the coordinate-biased convention that "slope" is "change-in-$y$ over change-in-$x$" (aka, "rise over run"). Nevertheless, vertical lines (in particular, vertical tangent lines) exist despite their algebraically problematic slopes. A way around the problem is to separate the "rise" and "run" components into a vector: $(\text{run},\text{rise})$. With this, either component can vanish yet still provide a meaningful description of the line's direction. Conveniently, a curve parameterized by $(x(t),y(t))$ has tangent vector $(x'(t),y'(t))$. – Blue Feb 17 '21 at 10:38
  • 1
    @Blue: Thank you, it does help to think of this phenomenon simply as a by-product of our coordinate system. I'm not that familiar with curve parameterisation. Is it possible if you give me an example of how $f: x \mapsto x^{1/3}$ can be parameterised? – Joe Feb 17 '21 at 10:48
  • See Wikipedia's "Parametric equations" entry; also, this ancient answer of mine. We parameterize an $xy$ relation by assigning $x$ and $y$ to be formulas in a third variable (say, $t$) that fit. Eg, circle $x^2+y^2=1$ can be parameterized by $(x,y)=(\cos t,\sin t)$, since $(\cos t)^2+(\sin t)^2=1$. Your relation $y=x^{1/3}$ can be parameterized by $(t^3,t)$ (which meets the origin when $t=0$); the tangent's direction vector is $(x',y')=(3t^2,1)$, which is non-problematically $(0,1)$ when $t=0$. – Blue Feb 17 '21 at 11:03
  • @Blue: It amazes me that you always have an existing answer that is pertinent to my question :) If you wish, you can turn your comments into an answer. – Joe Feb 17 '21 at 12:08

2 Answers2

3

You won't find a definition of the tangent line that is completely independent of the general concept of derivatives, since they are so intimately connected. But from the point of view of differential geometry, you can most certainly have vertical tangent lines. To this end, we have to slightly shift our point of view: we're not looking for tangent lines to the graph of a function, but to some smooth set of points, which happens to be easily described as the graph of a function. More rigorously, we're interpreting the graph as a smooth submanifold of $\mathbb R^2$. In this case, the tangent line at $p$ can be parameterized as $t_p(\tau)=p+\tau v$, where $v$ is a nonzero vector tangent to the manifold at $p$, in this case $(0,1)$, for instance. Of course, to find such a vector, we'll end up using derivatives anyway: we'd parametrize the manifold, say by the smooth curve $\gamma:\tau\mapsto(\tau^3,\tau)$, and then take its derivative at $\tau=\gamma^{-1}(p)$ (since $\tau=\gamma^{-1}(p)$ yields $p$ when inserted into $\gamma$). This derivative is a vector tangent to the parameterized curve/manifold at $p=0$.

Vercassivelaunos
  • 13,226
  • 2
  • 13
  • 41
  • Well, the ancient Greeks computed tangents without any notion of derivatives. – Michael Hoppe Feb 17 '21 at 15:45
  • 1
    @MichaelHoppe: Do you happen to know how they defined tangent lines? I suspect that a translation into the language of modern math would use some concepts that are at least related to derivatives. Similar to how Archimedes calculated to area enclosed by a parabola without a concept of integrals, but using methods very similar to modern lower and upper sums. – Vercassivelaunos Feb 17 '21 at 16:38
1

Your geometric intuition is sound. The problem about taking the derivative is an artifact of the coordinate system used to define it. This is solved in differential geometry where a space is covered by an atlas of compatible coordinate charts. This way, we can choose the right coordinate chart for the problem at hand. For example, to find the 'vertical tangent', we swap the coordinate axes, and find that this tangent is now 'horizontal'. Of course, the terms 'horizontal' and 'vertical' relate to our choice of chart. In more invariant geometric language, what we want to understand is how the curve actually curves in the plane. And what we see is that the location of your 'vertical tangent' is better described as the location of an inflection point

In differential geometry, you will see that both the geometric and derivational notion of a tangent dovetail exactly. In fact, this occurs so naturally, that in some treatments of differential geometry, it's the derivations - aka the derivative - that takes the starring role - as the development is simpler.

(In more sophisticated treatments of differential geometry for singular spaces or infinite-dimensional spaces it's seen that they diverge again, though of course there remains an intimate relationship. For example, in Michors & Kriegl conveniant calculus for infinite dimensional spaces it is the geometric tangent along curves that takes the starring role and the derivational is dispensed with. The same goes for Neeb's development of calculus in locally convex spaces (again it's the infinite-dimensional context that is important). In contrast, in Souriau's diffeology and developed by Isglesias-Zemmour (important for both infinite-dimensional and singular spaces and vastly more general than the foregoing), a notion of smoothness is introduced that is inspired from topology. Here, Christensen after correcting a definition by Hector and Laubinger, shows that there are distinct geometric and derivational tangent vectors. They are not the same here, but of course they are in many natural cases).

Mozibur Ullah
  • 6,113