2

  1. A bag I contain $4$ white and $6$ black balls while another Bag II contains $4$ white and $3$ black balls. One ball is drawn at random from one of the bags, and it is found to be black. Find the probability that it was drawn from Bag $I$.

  2. By using NLP, I can detect spam e-mails in my inbox. Assume that the word ‘offer’ occurs in $80$% of the spam messages in my account. Also, let’s assume ‘offer’ occurs in $10$% of my desired e-mails. If $30$% of the received e-mails are considered as a scam, and I will receive a new message which contains ‘offer’, what is the probability that it is spam?

I have drawn tree digram for both and it works for the first question but not for the second question

Can you explain it?

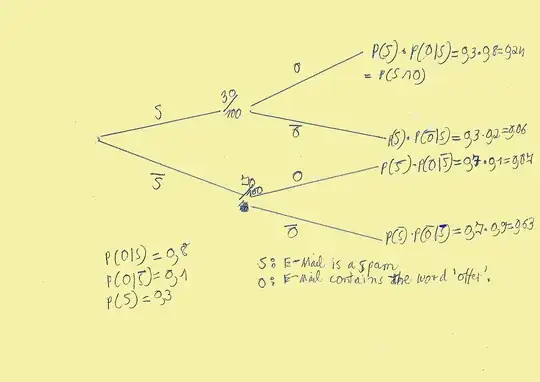
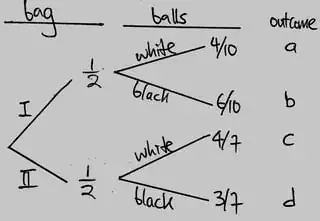
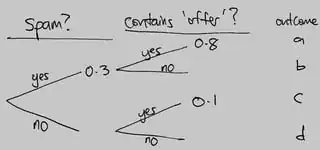
Thank you!enter image description here

vitamin d
  • 5,783
Jay
  • 45
  • 4

3 Answers3

4

The surprising thing is not that the second calculation is wrong, but that the first calculation is right.

You shouldn't be using probabilities in the diagram. Instead, you should be counting events. Let's look at the second diagram first. The idea is that we receive $100$ typical emails, so that $30$ are spam and $70$ are desired. Of the $30$ spam emails, $80\%$, or $24$ contain the word "offer" and $6$ do not. Of the $70$ desired emails, $7$ contain the word "offer" and $63$ do not. We have received $31$ emails containing the word "offer" and $24$ of them are spam. We conclude that the probability that an email is spam, given that it contains the word "offer" is $\frac{24}{31}$.

The first problem is peculiar. You are interpreting the phrase "A ball is drawn at random from one of the bags," to me that each of the $17$ balls has an equal probability of being selected. So, if we do this $17$ times, we'll draw $9$ black balls, $3$ from bag II and $6$ from bag $I$ and $$\Pr(I|B)=\frac23$$ if we ignore the denominators in the diagram. How come the book says the answer is $\frac7{12}$? I believe they intend that one of the bags be chosen at random, and then a ball be chosen at random from that bag. Bayes' rule rule gives $$\begin{align} \Pr(I|B)&=\Pr(B|I)\frac{\Pr(I)}{\Pr(B)}\\ &=\frac{\Pr(B|I)\Pr(I)}{\Pr(I)\Pr(B|I)+\Pr(II)\Pr(B|II)}\\ &=\frac{\frac{6}{10}\cdot\frac12}{\frac12\cdot\frac6{10}+\frac12\cdot\frac37}\\ &=\frac{\frac{6}{10}}{\frac6{10}+\frac37}=\frac{42}{42+30}=\frac7{12}\\ \end{align}$$

saulspatz
  • 53,131
1

My tree diagram looks like the following:

enter image description here

Then it is asked for $P(S|O)=\frac{P(O\cap S)}{P(O)}=\frac{0.24}{0.24+0.07}$. It is all comprehensible? If not, feel free to ask.

callculus42
  • 30,550
1

Question 1:enter image description here $$P(\text{bag I | black ball})\\= \frac{P(\{b\})}{P(\{b,d\})}\\= \frac{\frac12\times\frac6{10}}{\frac12\times\frac6{10}+\frac12\times\frac37}\\= \frac7{12}$$

Question 2:enter image description here $$P(\text{spam | contains ‘offer’}) \\= \frac{P(\{a\})}{P(\{a,c\})}\\= \frac{0.3\times0.8}{0.3\times0.8+(1-0.3)\times0.1}\\= \frac{24}{31}$$

Notice that:

  1. the outcomes (the rightmost column) of an experiment constitute the sample space;
  2. each event is a subset of the sample space: e.g., the event of obtaining a black ball $=\{b,d\};$
  3. the probability of a given outcome, say, $d,$ is obtained by multiplying the values on all the branches leading to it;
  4. the values on the branches of a probability tree are conditional probabilities;
  5. point (4) justifies why point (3) applies even when the trials (the underlined columns) are dependent, as in the two examples above;
  6. abusing notation, $P(\{b,d\})$ and $P(\{HH,HT\})$ are typically simply written as $P(b,d)$ and $P(HH,HT)$.
ryang
  • 38,879
  • 14
  • 81
  • 179