1

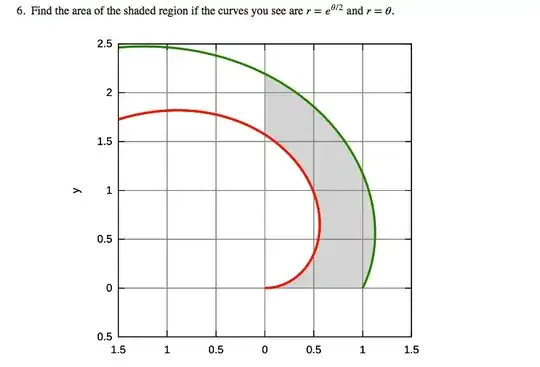
enter image description here

That's the picture of the shaded region I have to find the area of. I'm totally stuck on this problem mainly because these two curves don't intersect so I'm not sure how to find the bounds of integration. Once I find those my guess would be to the outside curve - the inside curve and just do the integration from there.

Américo Tavares
  • 38,602
barndog
  • 131
  • 1
  • 4
  • The poser of the problem was nice to you because the lines terminating the area point to the right and upward from the origin, so the limits of integration for the area will be $ \ \theta = 0 \ $ and $ \ \theta = \frac{\pi}{2} \ $ . [Don't forget that you want to integrate $ \ (\frac{1}{2} r(\theta)^2_{outer}) \ - \ (\frac{1}{2} r(\theta)^2_{inner}) \ . ] $ – colormegone May 28 '13 at 19:50
  • You presumably know the formula for area in polar coordinates. Here we have the difference of two areas that are not hard to find. – André Nicolas May 28 '13 at 19:54
  • 2
    Oh. Well that's stupid easy. facepalm thanks people. – barndog May 28 '13 at 19:55
  • 1
    It's all right -- polar area integration problems aren't always done between intersection points... – colormegone May 28 '13 at 20:11

1 Answers1

1

We have to find the area of the region $R$ between $r=\theta $ and $r=e^{\theta/2}$, and between $\theta =0$ and $\theta =\pi /2$. Since the Jacobian of the transformation from Cartesian to polar coordinates is $r$, the area $A$ is given by the double integral (see Explain $\iint \mathrm dx\,\mathrm dy = \iint r \,\mathrm \,d\alpha\,\mathrm dr$): $$ \begin{eqnarray*} A &=&\iint_{R}dA=\int_{0}^{\pi /2}\left( \int_{\theta }^{e^{\theta /2}}r\;dr\right)\ d\theta \\ &=&\int_{0}^{\pi /2}\big( \frac{e^{\theta }}{2}-\frac{\theta ^{2}}{2} \big)\ d\theta \\ &=&\frac{1}{2}\int_{0}^{\pi /2}e^{\theta }d\theta -\frac{1}{2}\int_{0}^{\pi /2}\theta ^{2}\ d\theta \\ &=&\big( \frac{e^{\pi /2}}{2}-\frac{1}{2}\big) -\frac{\pi ^{3}}{48}. \end{eqnarray*} $$

Community
  • 1
Américo Tavares
  • 38,602