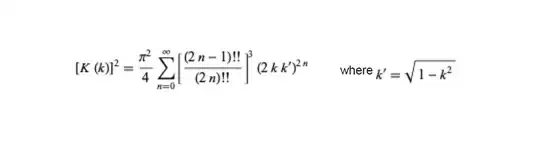It's true that $\displaystyle \int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}} \frac{2}{\sqrt{1-\sin^2\theta\sin^2\phi}} d\phi d\theta =\int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}} \frac{1}{\sqrt{\sin\theta\sin\phi}} d\phi d\theta$ ?
If yes, I need a way to prove the equality of the following two integrals
I tried everything but I am unable to convert into a standard form so How do I solve this problem.
Addition 1: For the second integral $\int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}} \frac{1}{\sqrt{\sin\theta\sin\phi}} d\phi d\theta =\bigg(\int_0^{\frac{\pi}{2}}\frac{1}{\sqrt{\sin\theta}}d\theta\bigg)^2 $ and we can use that $2 \int^{\frac{\pi}{2}}_{0}\frac{1}{\sqrt{\sin x}} \mathrm dx = \frac{\Gamma(1/2)\Gamma(1/4)}{\Gamma(3/4)} = \frac{\Gamma \left( \frac{1}{4}\right)^2}{\sqrt{2\pi}}$
Addition 2: For the first integral
Let $\displaystyle K(k)=\int_0^{\frac{\pi}{2}}\frac{1}{\sqrt{1-k^2\sin^2 t}}dt$ ( Complete Elliptic Integral of the First Kind). we know that $ \displaystyle K(k)=\frac{\pi}{2}\sum_{n=0}^\infty \left(\frac{(2n)!}{2^{2n}(n!)^2}\right)^2k^{2n}$. Then it's not difficult de show that $\int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}} \frac{1}{\sqrt{1-\sin^2\theta\sin^2\phi}} d\phi d\theta=(\pi /2 )^2 \sum _{n=0}^{\infty }(\frac{(2n)!}{4^n(n!)^2})^3$.
The egality of the two integrals hold if we can calculte $$\sum _{n=0}^{\infty }(\frac{(2n)!}{4^n(n!)^2})^3$$ Wolfram gives
Addition 3: