How can I prove that $f(x) = \left(1 + \frac1x \right)^x$ is concave in $\mathbb{R}^+$?

Question

$$f(x) = \left(1 + \frac1x \right)^x$$

In general, attempting to demonstrate that

$$f(ax + (1-a)y) \ge af(x) + (1-a)f(y)$$

leads to algebraically difficult expressions with no clear resolution.

I am aware that we can attempt to show $f''(x) \le 0$. We have:

$$f''(x) = \left(1+\frac{1}{x}\right)^x \left(\log\left(1+\frac{1}{x})\right) - \frac{1}{x\left(1+\frac{1}{x}\right)}\right)^2 - \frac{\left(1+\frac{1}{x}\right)^{x-2}}{x^3} \le 0$$

If we (1) add the second term to both sides, (2) multiply by $x^3$, (3) divide by $(1+1/x)^{x-2}$, (4) take a square root, and (5) multiply the $(1+1/x)$ through the parentheses on the LHS, we arrive at:

$$x^{3/2} \left(\left(1+\frac{1}{x}\right)\log\left(1+\frac{1}{x}\right) - \frac{1}{x}\right) \le 1$$

From here, it is again unclear how to proceed.

Answer 1

I was waiting for someone to post a more clever answer, but since one doesn't seem to be coming I'll post this anyways. Hopefully it doesn't discourage someone else from seeing this question and posting something more elegant. If nothing else, this is how I would solve the problem if it came up in my research.

Showing this function is convex is certainly tedious, but the tedium is remedied somewhat by the use of a computer algebra system such as sage.

Indeed, we can try

sage: f(x) = (1+1/x)^x
sage: secondDerivative = diff(f,x,2)
sage: secondDerivative
x |--> (1/x + 1)^x*(1/(x*(1/x + 1)) - log(1/x + 1))^2 - (1/x + 1)^x/(x^3*(1/x + 1)^2)
sage: plot(secondDerivative)

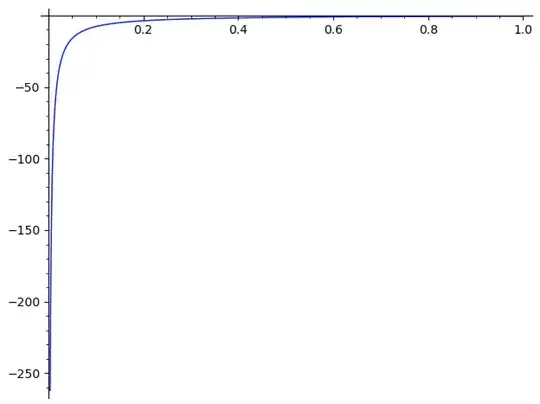
This certainly seems to be negative everywhere, but we should confirm the behavior as $x \to 0^+$ and as $x \to \infty$.

sage: lim(secondDerivative, x=0, dir='+')
x |--> -Infinity
sage: lim(secondDerivative, x=oo)
x |--> 0

This is good evidence, but we should probably be more precise.

sage: view(secondDerivative)

gives us

$$ \newcommand{\Bold}[1]{\mathbf{#1}}x \ {\mapsto}\ {\left(\frac{1}{x} + 1\right)}^{x} {\left(\frac{1}{x {\left(\frac{1}{x} + 1\right)}} - \log\left(\frac{1}{x} + 1\right)\right)}^{2} - \frac{{\left(\frac{1}{x} + 1\right)}^{x}}{x^{3} {\left(\frac{1}{x} + 1\right)}^{2}} $$

Of course, we as humans can quickly make some simplifications that sage missed, and we rewrite this as

$$ \left ( 1 + \frac{1}{x} \right )^x \left [ \left ( \frac{1}{1+x} - \log \left ( 1 + \frac{1}{x} \right ) \right )^2 - \frac{1}{x^3 + 2x^2 + x} \right ] $$

We know $(1+\frac{1}{x})^x$ is positive when $x$ is, so the sign of the second derivative is governed by the second factor. We'd like to show it's negative, but sage prefers rational functions to transcendental ones... Thankfully, you may remember that (for $x > -1$)

$$ \frac{x}{1+x} \leq \log(1+x) \leq x $$

So if we evaluate the lower bound at $\frac{1}{x}$, we get an upper bound for our expression of interest (since we're subtracting $\log(1+1/x)$). This gives

$$ -\log(1+1/x) \leq - \frac{1}{1+x} $$

So our expression of interest is at most

$$ \left ( \frac{1}{1+x} - \frac{1}{1+x} \right )^2 - \frac{1}{x^3 + 2x^2 + x} $$

which is

$$ - \frac{1}{x^3 + 2x^2 + x} $$

and in the interest of offloading as much thinking as possible to the computer (though this is of course easy to do by hand):

sage: solve(-1/(x^3 + 2*x^2 + x) < 0)
[[x > 0]]

So this is negative everywhere of interest, and our function is concave.

---

I know this answer looks really long, but that's because I was trying to explain step-by-step how I would attack the problem. You can imagine this is fairly quick to do by yourself. In general, computer algebra systems are great at these sorts of questions, and it's worth learning how to use one for exactly situations like this!

---

I hope this helps ^_^