1

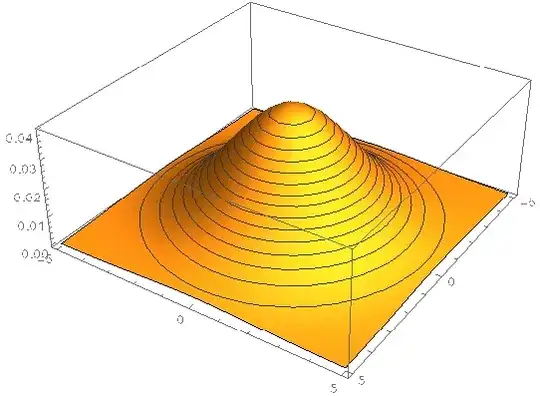
Suppose that $X, Y \sim N(0, 4)$ are independent and normally distributed random variables.

My question is how to find $P(2 \leq |X| + |Y| \leq 3)$?

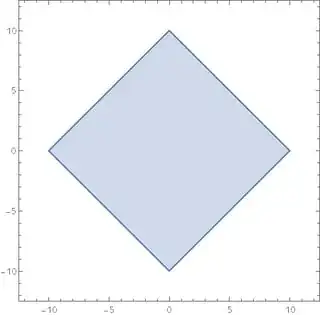
Probably, the first step is to try to solve a more general task and find the distribution of $Z := |X| + |Y|$, i.e. find $F_Z(t) = P(Z \leq t) = P(|X| + |Y| \leq t)$ for $t > 0$.

The straightforward way would be to compute the integral:

$$\int\limits_{|x| + |y| \leq t} \dfrac{1}{8\pi} e^{-(x^2 + y^2)/4}dxdy$$

This task seems to be non-trivial because the resulting integrals end up being hard to calculate. Assuming the function $\Phi(t) = \int\limits_{-\infty}^{t} \dfrac{1}{\sqrt{2\pi}}e^{-x^2/2}dx$ is known, the integral above requires computing something like $\int\limits_{0}^{t}e^{-x^2/4}\Phi(x) dx$ which I'm not sure how to compute with simple calculus tools that I know.

Maybe it is easier than I think or maybe there is just a different better way of solving this.

Any help would be greatly appreciated.

Swistack
  • 802
  • 2
    The distribution of the absolute value of a normal random value is a half-normal distribution. Have a look here: https://math.stackexchange.com/questions/428781/sum-of-independent-folded-normal-distributions – hgmath Mar 23 '21 at 19:59
  • @hgmath Thank you for the reference! But in this answer https://math.stackexchange.com/a/428790/251704 I haven't quite understood the point about circular symmetry. That would great if you could kindly elaborate, why can we just use the rotated square instead of the original one? – Swistack Mar 24 '21 at 09:37
  • 1
    ok, I will try to write it (in an answer) – hgmath Mar 24 '21 at 20:42

1 Answers1

3

As asked for in a comment I'll try to elaborate on the "circular symmetry" argument given in this answer.

Basically we are given two normally distributed, independent random variables $X,Y \sim N(0,4)$ and want to find the distribution function of $|X|+|Y|$. I.e. for $a>0$ we want to calculate $$F_{|X|+|Y|}(a) = P(|X|+|Y|\leq a) $$ This means that we want to find the probability of $(X,Y)$ to lie within the set $$A = \{(x,y)\in\mathbb{R}^2 \mid |x|+|y|\leq a\} .$$ Geometrically $A$ is a square with corners at $(-a, 0)$, $(0, -a)$, $(a, 0)$ and $(0, a)$. For example, with $a=10$:

square

Now, because $X$ and $Y$ are independent, the random vector $(X,Y)$ is jointly normal-distributed with covariance matrix $\begin{pmatrix}4&0\\0&4\end{pmatrix}$. This means that it is rotationally invariant: for every angle $\alpha$, the rotated vector $$\begin{pmatrix} \cos \alpha& -\sin \alpha \\ \sin \alpha & \cos \alpha \\ \end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix}$$ has the same distribution as the vector $(X,Y)$ itself. (This can be checked using how a multivariate normal distribution changes under a linear transformation; note that the rotation matrix is orthogonal.) The symmetry can also be seen geometrically by plotting the density:

pdf

Hence, denoting the rotation by $\alpha$ as $R_\alpha$, $$P((X,Y) \in A) = P(R_{-\alpha}(X,Y) \in A) = P((X,Y) \in R_\alpha(A)) .$$

We can thus equivalently compute the probability of $(X,Y)$ lying in the rotated square $A'$. Now choose $\alpha=45^\circ$; rotating the square by $45^\circ$ yields a square with axis parallel sides (the side lengths remains the same: $\sqrt{2}a$)

square2

And now $$P((X,Y) \in A') = P\left(|X|\leq \frac{\sqrt{2}a}{2}, |Y|\leq \frac{\sqrt{2}a}{2}\right) = \left(F_{N(0,4)}\left(\frac{\sqrt{2}a}{2}\right) - F_{N(0,4)}\left(-\frac{\sqrt{2}a}{2}\right)\right)^2 .$$

hgmath
  • 1,830