Evaluate $\lim_{h \to 0} \frac{\sin(\frac{h}{2})-\frac{h}{2}}{h\sin(\frac{h}{2})}$ without l'Hospital

Question

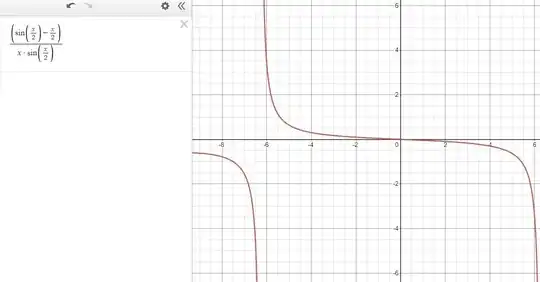
$$ \lim_{h \to 0} \frac{\sin(\frac{h}{2})-\frac{h}{2}}{h\sin(\frac{h}{2})} $$

I've worked the last few hours on this equation and still didnt find a way to evaluate it. The idea I had was to bound this expression like this:

$$ ? \leqslant \lim_{h \to 0} \frac{\sin(\frac{h}{2})-\frac{h}{2}}{h\sin(\frac{h}{2})}\leqslant0 $$

If you could guide me maybe to find this expression or guide me on another track. Thanks in advance !

Answer 1

Let $x=h/2$. Famously (proven e.g. here without any off-limits methods), $\lim_{x\to0}\frac{\sin x-x}{x^3}=-\tfrac16$. Since even more famously $\lim_{x\to0}\frac{\sin x}{x}=1$, you want$$\lim_{x\to0}\frac{\sin x-x}{2x\sin x}=\lim_{x\to0}\frac{\sin x-x}{2x^2}=0.$$

Answer 2

Use Taylor series as needed. Numerator $\approx \frac{-(h/2)^3}{3!}$, denominator $\approx \frac{h^2}{2}$. Ratio $\to 0$ as $h\to 0$..

Answer 3

This question can be solved by using the expansion of the function $\sin x$ which is as $$\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ \cdots $$

Thus substituting $\frac{h}{2}$ in place of $x$ and then solving accordingly will give the answer.