The plane equation is not right. The points satisfying parametrization you gave live on the paraboloid $z = 4x^2 +y^2$, they only intersect the plane at some points.
Well if you wanna use divergence theorem:
The integration region is as follows:
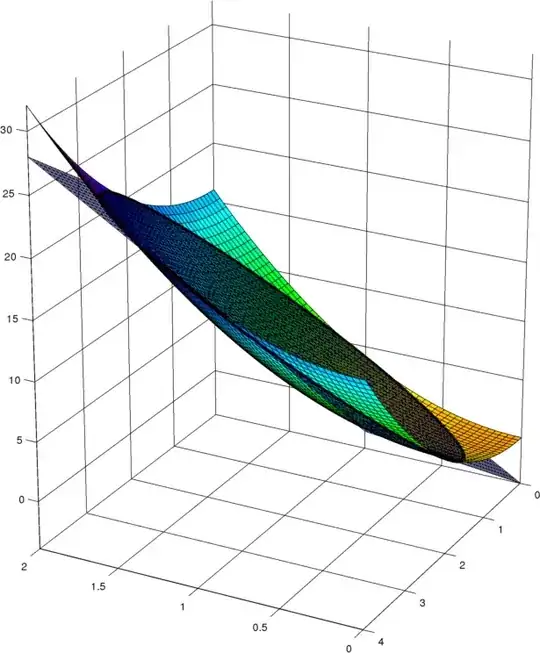
The bottom is the surface $z=4x^2+y^2$, while it has a cap formed by the plane $z=8x+4y−4$. Equaling the right sides of these two we find the intersecting curve is:
$$
\{(x,y,z): (x-1)^2 + (y-2)^2/2 = 1,\; z=8x+4y−4\}.
$$
Now the cap surface is:
$$
C = \{(x,y,z): (x-1)^2 + (y-2)^2/2 < 1,\; z=8x+4y−4\}.
$$
Its unit normal vector (choose the one pointing upward) is $n_C =(-8/9,-4/9,1/9)$.
The bottom surface is:
$$
S = \{(x,y,z): (x-1)^2 + (y-2)^2/2 < 1,\; z=4x^2+y^2\}.
$$
Let the region bounded by $C$ and $S$ be $V$, $F = (x,y,3z)$, then by divergence theorem:
$$
\int_V \nabla \cdot F\,dV = \int_{\partial V} F\cdot n \,dS = \int_{C} F\cdot n_C \,dS + \int_{S} F\cdot n_S \,dS,
$$
here the normal to $S$ is point downward, if choosing the pointing upward one $n_S = -n$, we have:
$$
\int_{S} F\cdot n_S \,dS = \int_{C} F\cdot n_C \,dS - \int_V \nabla \cdot F\,dV.\tag{1}
$$
Now
$$
F\cdot n_C\bigg|_C = -\frac{8}{9}x - \frac{4}{9}y + \frac{1}{3}z = \frac{2}{9}z - \frac{4}{9},
$$
and we can parametrize the elliptical cap $C$ by
$$\begin{cases} x - 1 = r\cos t, \\ y-2 = \sqrt{2}\,r \sin t,\end{cases}\tag{2}$$
where $0<r<1$, and $t\in (0,2\pi)$, $z = 8(1+r\cos t) + 4(2+ \sqrt{2}\,r \sin t) -4$, the Jacobian $J$ is left for you to compute, then the integral becomes:
$$
\int_{C} F\cdot n_C \,dS = \int^{2\pi}_0\int^1_0\left( \frac{2}{9}\big(8(1+r\cos t) + 4(2+ \sqrt{2}\,r \sin t) -4\big) - \frac{4}{9}\right) |J| \,dr\,dt.\tag{3}
$$
Divergence of $F$ is $5$, so
$$
\begin{aligned}
&\int_V \nabla \cdot F\,dV = 5 \iint_{(x-1)^2 + (y-2)^2/2 < 1}\int^{8x+4y-4}_{4x^2+y^2}\,dz\,dx\,dy
\\
=& 5 \iint_{(x-1)^2 + (y-2)^2/2 < 1} \left( \big(8x+4y-4\big) - \big(4x^2+y^2\big)\right)\,dx\,dy
\\
=& 5 \iint_{(x-1)^2 + (y-2)^2/2 < 1} \left( 2 - 2(x-1)^2 - (y-2)^2\right)\,dx\,dy
\\
=& 5\int^{2\pi}_0\int^1_0 \left( 2 - 2r^2 \cos^2 t - 2r^2 \sin^2 t\right) |J|\,dr\,dt.\tag{4}
\end{aligned}
$$
What left for you to do: Compute the Jacobian from (2), then evaluate (3) and (4) to get (1), the left side of (1) is what you wanna evaluate.
