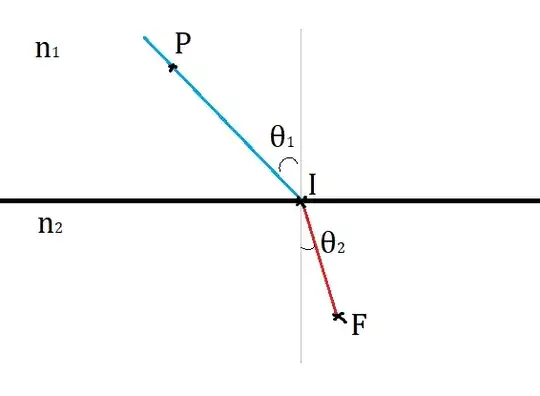
I am simulating the phenomenon of refraction, ruled by Snell's law: $$\sin\theta_1\cdot n_1 = \sin\theta_2\cdot n_2$$
For this question, is enough to know that relationship between both angles. $n_1$ and $n_2$ are given constants. The thick black line is called "interface".
What I am trying to achieve:
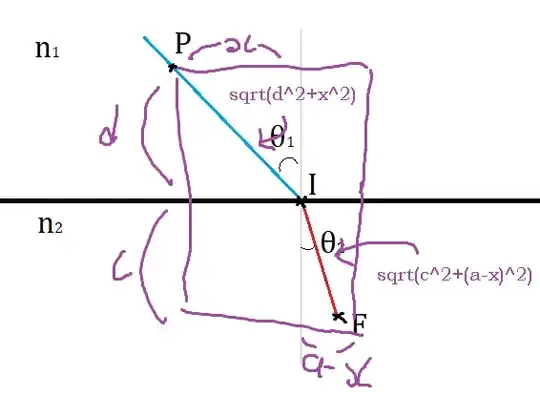
Based on user input, I know the coordinates of the point $P$ and point $F$ is fixed. Now, to draw the lines shown above, I need to determine where is the point $I$.
Specifically, I need to know its $x$ coordinate: the horizontal distance between $P$ and $I$.
How I tried to do it:
Since I know the horizontal distance between $P$ and $F$, I can equate it to the sum of the opposing legs of two right triangles, formed by angles $\theta_1$, $\theta_2$ and the vertical thin line, as shown below:
$$P_y\cdot\tan{\theta_1}+F_y\cdot\tan{\theta_2}=F_x - P_x$$
(Assuming absolute values and the interface is located at $y=0$).
Using Snell's law, I found that $\sin{\theta_2}=\frac{n_1}{n_2}\sin{\theta_1}$. Then, I tried to substitute it in the equation above. To simplify the expression, let $m=\frac{n_1}{n_2}$.
The issue
In terms of $\sin{\theta_1}$, the equation becomes:
$$P_y\frac{\sin{\theta_1}}{\sqrt{1-\sin^2{\theta_1}}}+F_y\frac{m\sin{\theta_1}}{\sqrt{1-m^2\sin^2{\theta_1}}}=F_x - P_x$$
And I'm stuck here. WolframAlpha could not help, and I don't know any numerical method good enough to determine $\sin{\theta_1}$. How can I solve that equation for $\sin{\theta_1}$?