1

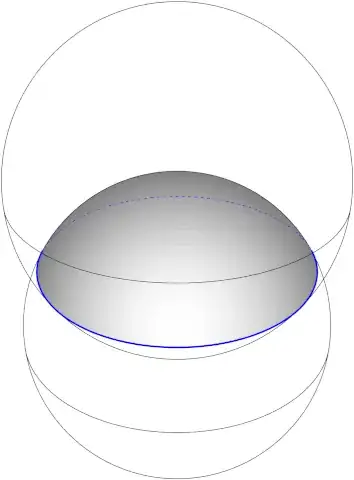
Why do we say that if two solid spheres intersect, the result will be as follows ?

https://bit.ly/34NRMTF

  1. Empty ( Right, because everything is possible in reality plus virtuality)

  2. Point (Right, because they touch at one single point)

  3. Sphere (Right, if they both are same and fully cover each other)

  4. Circle (I consider it wrong, correct me if I am wrong, because this is just a part of 3d leaf shape that forms when they intersect, not a formation in itself).

So, I think that circle isn't a full formation but infact we should count the three dimensional lens/leaf as fourth shape formed on intersection.

I think that may be because mathematical solving of two sphere equations gives circle as a result. I don't know if 3d leaf is a solution or not (is it because I didn't find it anywhere?) but that's common sense upon visualization. For e.g. if there are two equations :

  1. Y = $x^2$
  2. Y = X

If we solve them, solutions are (0,0) and (1,1). But we can't say that their intersection forms two points but we have to look at shape formed by their intersection, that's what really is formed, not points (as in case with spheres, circle is where collection of points where they intersect, not the shape itself).

Please explain to me why we include circle in those 4 shapes. Am I wrong or not?

Nikhil Sharma
  • 19
  • In the language of topology, 2-sphere refers to surface only. 3-ball refers to solid. Intersections for two categories are different. – Ng Chung Tak Jun 05 '21 at 12:31

2 Answers2

2

In mathematics, a sphere is generally taken to mean the surface of a solid sphere (which is called a ball). So in three dimensions, the equation $$x^2+y^2+z^2=r^2$$ defines a sphere of radius $r$; the inequality $$x^2+y^2+z^2< r^2$$ defines an open ball of radius $r$ (the closed ball is defined by $x^2+y^2+z^2\le r^2$).

TonyK
  • 64,559
  • I think the issue is indeed with ball instead of sphere but as well with the "lens shape" of the intersection. – Jean Marie Jun 05 '21 at 12:17
  • 1
    But @JeanMarie, the intersection of two spheres is not lens-shaped. That would be the intersection of two balls. – TonyK Jun 05 '21 at 12:25
  • It is evidently what I mean (and what the OP means without using the right term). – Jean Marie Jun 05 '21 at 12:28
  • @TonyK If "sphere" is collection of only surface points even then shape will lens shaped albeit "hollow lens shape". But the shape will look only like that. In ball's case, it will mean "solid lens shape". Explain, if I am misunderstanding. – Nikhil Sharma Jun 05 '21 at 12:39
  • Ok, I understood now. If the sphere 2 goes inside the sphere 1 , it will be outside the scope of sphere 1, right? That thing will fall in line with range of sphere 2, right? But the circle (https://en.m.wikipedia.org/wiki/Circle_of_a_sphere) will be inside the scope of sphere 1, right (on surface)? – Nikhil Sharma Jun 05 '21 at 12:47
1

In the hope a picture is worth a thousand words, the blue curve is the intersection of the spheres shown, while the gray shaded cap is the intersetion of the lower sphere with the upper solid ball.

The intersection of two spheres

Andrew D. Hwang
  • 78,195